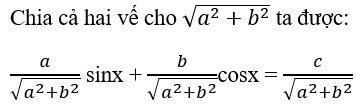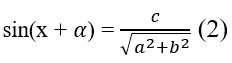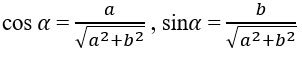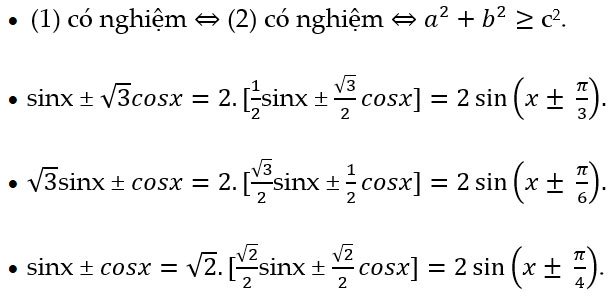[Toán 11] Phương trình lượng giác cơ bản và các dạng thường gặp

Ở bài trước chúng ta đã học về Hàm số lượng giác và các dạng bài tập thường gặp. Trong bài viết hôm nay, chúng ta sẽ tiếp tục đi sâu hơn vào  Phương trình lượng giác cơ bản và các dạng thường gặp trong chương trình Toán học. Cùng congthuctoanlyhoa học ngay thôi nào!

Các phương trình lượng giác cơ bản

Phương trình sin x = a

• Nếu |a| > 1 => Phương trình vô nghiệm
• Nếu |a| ≤ 1:
• Tổng quát:

Lưu ý, các trường hợp đặc biệt

sin x = 0 ⟺ x = kπ (k ∈ Z)

sin x = 1 ⟺ x = π/2 + k2π (k ∈ Z)

sin x = -1 ⟺ x = -π/2 + k2π (k ∈ Z)

sin x = ±1 ⟺  sin²x = 1 ⟺  cos²x = 0 ⟺ cos x = 0 ⟺  x = π/2 +kπ (k ∈ Z)

Phương trình cos x =  a

• Nếu |a| > 1 => Phương trình vô nghiệm
• Nếu |a| < 1:

cos x = cos α ⟺ x =±α + k2π (k ∈ Z)

cos x = cos β⁰ ⟺ x = ±β + k360⁰ (k ∈ Z)

cos x = a ⟺ x = ±arccosa + k2π (k ∈ Z)

• Tổng quát: cos f(x) = cos g(x) ⟺ f(x) = ±g(x) +k2π (k ∈ Z)
• Lưu ý các trường hợp đặc biệt:

cos x = 0 ⟺ x = π/2 + kπ (k ∈ Z)

cos x = 1 ⟺ x = k2π (k ∈ Z)

cos x = -1 ⟺ x = π + k2π (k ∈ Z)

cos x = ±1 ⟺ cos²x = 1 ⟺ sin²x = 0 ⟺ sin x = = ⟺ x = kπ (k ∈ Z)

Phương trình tan x = a

tan x = tan α ⟺ x = α + kπ (k ∈ Z)

tan x = tan β⁰ ⟺ x = β⁰ +k18⁰ (k ∈ Z)

tan x = a ⟺ x = arctan a + kπ (k ∈ Z)

• Tổng quát: tan f(x) = tan g(x) ⟺ f(x) = g(x) + kπ (k ∈ Z)
• Lưu ý các trường hợp đặc biệt:

tan x = 0 ⟺ x = kπ (k ∈ Z)

tan x= ±1 ⟺ x = ±π /4 + kπ (k ∈ Z)

Phương trình cot x = a

cot x = cot α ⟺ x = α + kπ (k ∈ Z)

cot x = cot β⁰ ⟺ x  = β⁰ + k180⁰ (k ∈ Z)

cot x = a ⟺ x = arc cot a + kπ (k ∈ Z)

• Tổng quát: cot f(x) = cot g(x) ⟺  f(x) = g(x) + kπ (k ∈ Z)
• Lưu ý các trường hợp đặc biệt:

cot x = 0 ⟺ x = π/2 + kπ (k ∈ Z)

cot x = ±1 ⟺ x = ±π/4 + kπ (k ∈ Z)

Bên cạnh các phương trình lượng giác cơ bản, trong chương trình Đại số lớp 11, chúng ta cũng cần phải ghi nhớ và làm quen với một số dạng phương trình lượng giác sau đây

Phương trình bậc nhất đối với một hàm số lượng giác

Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng at + b = 0 trong đó a,b là các hằng số ( a ≠ 0) và t là một trong các hàm số lượng giác.

Ví dụ: 3sinx – 1 = 0; cos2x – 1/2 = 0; 2tanx – 1 = 0

Phương pháp làm bài: đưa về phương trình lượng giác cơ bản

Phương trình bậc hai đối với sin x, cos x, tan x, cot x

Dạng phương trình

Ta có các dạng phương trình bậc hai sau đây:

asin²x + bsin x + c = 0

acos²x + bcos x + c = 0

atan²x + btan x + c = 0

acot²x + bcot x + c = 0

Phương pháp làm bài

Để giải các phương trình bậc hai ở trên ta làm như sau:

• Đối với sin x => Đặt t = sin x(-1≤ t ≤ 1)
• Đối với cos x =>Đặt t = cos x(-1≤ t ≤ 1)
• Đối với tan x => Đặt t = tan x
• Đối với cot x => Đặt t = cot x

Sau đó ta giải tương tự như cách làm các phương trình bậc hai ở lớp dưới đã được học. Ngoài ra, đối với các bài tập trắc nghiệm ta cũng có thể bấm nhanh bằng máy tính

Lưu ý 

• Nếu a là một số cho trước mà tan α xác định thì phương trình tan x = tan a có nghiệm x = α + kp thỏa điều kiện cos x ≠ 0
• Phương trình tanP(x) = tanQ(x) thì cần phải chú ý đến điều kiện cosP(x) ≠ 0 và cosQ(x) ≠ 0

Phương trình bậc nhất đối với sin x và cos x

Dạng phương trình

Phương trình bậc nhất đối với sin x và cos x có dạng

a sin x + b cos x = c (1)

Điều kiện để phương trình có nghiệm: a2 + b2 ≥ c2

Phương pháp làm bài

Khi đó phương trình (1) được đưa về dạng

Ở đó α là cung thỏa mãn

Chú ý:

Tổng kết

Như vậy, Công Thức Toán Lý Hóa vừa gửi đến bạn đọc kiến thức về các phương trình lượng giác cơ bản và một số thường gặp trong chương trình Toán học lớp 11. Hy vọng các bạn đã ghi chép thật đầy đủ và luyện tập để sử dụng thành thạo các phương pháp này. Hẹn gặp lại các bạn trong những bài học lần sau.