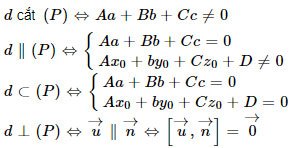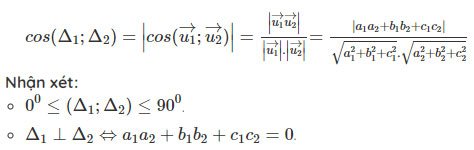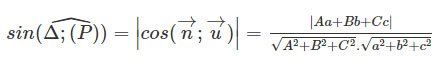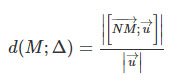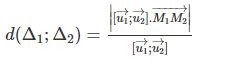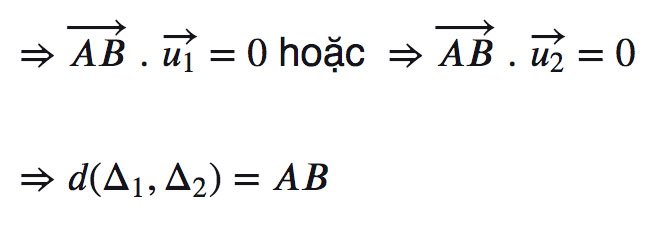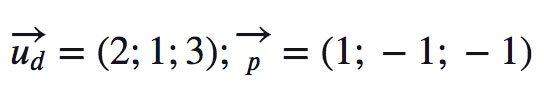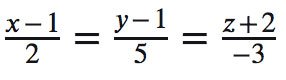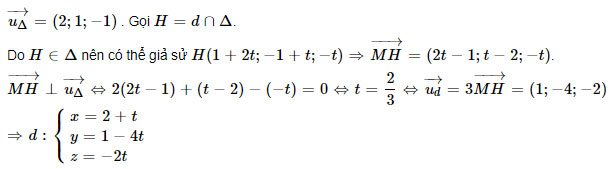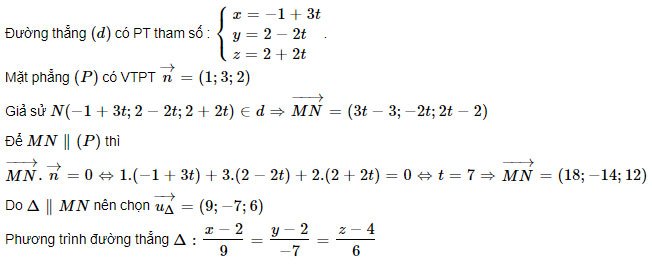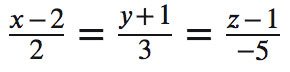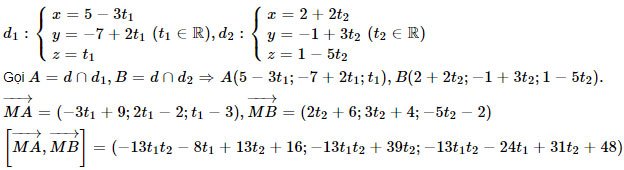Phương trình đường thẳng trong không gian là bài học cuối cùng trong phân môn Hình học 10. Phương trình sẽ được biểu diễn dưới 2 dạng chính là phương trình tham số và phương trình chính tắc. Bài viết này sẽ giúp các em biết cách xác định vectơ chỉ phương của đường thẳng và viết được phương trình trong trường hợp phổ biến. Bên cạnh đó, các cách tính khoảng cách, góc, xác định vị trí tương đối trong không gian có liên quan đến đường thẳng sẽ được congthuctoanlyhoa giới thiệu.
Phương trình tham số của đường thẳng
Đường thẳng d đi qua M0(x0;y0;z0) và vecto chỉ phương
Phương trình tham số d:
x=x0+at
y=y0+bt
z=z0+ct
(tϵR)
Phương trình chính tắc của đường thẳng trong không gian
Đường thẳng d đi qua M0(x0;y0;z0) và vecto chỉ phương
Phương trình tham số d:
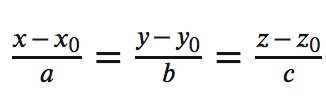
Vị trí tương đối giữa các đường thẳng
Trong không gian cho 2 đường thẳng 1 đi qua M1 và có một vecto chỉ phương u→. Khi đó vị trí tương đối Δ1 và Δ2 được xác định như sau:
Vị trí tương đối của đường thẳng với mặt phẳng
Đường thẳng d đi qua M0(x0;y0;z0) và có vectơ chỉ phương 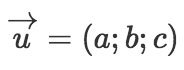
. Khi đó:
Góc giữa hai đường thẳng
Trong không gian cho 2 đường thẳng Δ1 có một vecto chỉ phương 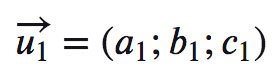
Góc giữa đường thẳng và mặt phẳng
Trong không gian cho đường thẳng Δ có vecto chỉ phương 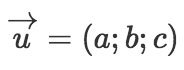
Các công thức tính khoảng cách liên quan đến đường thẳng
Sau đây, là một số công thức để tìm ra khoảng cách trong bài học thuộc phân môn Hình học 12.
Khoảng cách từ 1 điểm đến đường thẳng
Cho điểm M và đường thẳng Δ đi qua N và có một VTCP u. Khi đó, khoảng cách từ M đến Δ xác định bởi công thức:
Khoảng cách giữa hai đường thẳng chéo nhau
Cách 1:
Trong không gian cho đường thẳng Δ1 đi qua M1 có vecto chỉ phương u1→.Δ2 đi qua M2 có vecto chỉ phương u2→. Khi đó:
Cách 2:
Gọi AB là đoạn thẳng vuông góc Δ1,Δ2 với AϵΔ1,BϵΔ2
Các dạng bài tập về viết phương trình đường thẳng trong không gian
Dạng 1: Viết phương trình đường thẳng bằng cách xác định vectơ chỉ phương
Ví dụ 1: Với tọa độ Oxyz trong không gian cho đường thẳng
d: 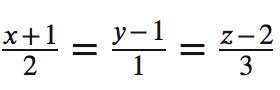
Giải
Để tìm được vectơ chỉ phương của Δ ta phải tìm 2 vectơ chỉ phương không cùng phương của nó sau đó tìm tích có hướng của 2 vecto.
Như vậy ta có: 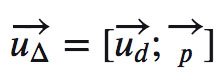
Trong đó:
Δ đi qua A(1; 1; -2) và có vectơ chỉ phương
⇒ Ta có phương trình: Δ:
Ví dụ 2:
Cho tọa độ Oxyz trong không gian cho đường thẳng Δ: 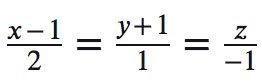
P: x−y−z−1=0. Viết phương trình đường thẳng d vuông góc và cắt với Δ, qua M(2; 1; 0).
Giải:
Dạng 2: Viết phương trình đường thẳng liên quan đến một đường thẳng khác
Ví dụ 1: Cho tọa độ Oxyz trong không gian cho đường thẳng d: 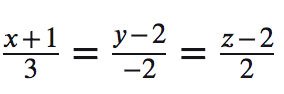
Giải:
Dạng 3: Viết phương trình đường thẳng liên quan đến một đường thẳng khác
Ví dụ 1: Cho hệ tọa độ Oxyz trong không gian, viết phương trình của đường thẳng d đi qua điểm M(-4; -5; 3) và cắt cả 2 đường thẳng d1:2x+3x+11=0 hoặc y−2z+7=0 và d2:
Giải:
Viết phương trình đường thẳng:
Dạng 4: Viết phương trình đường thẳng liên quan đến khoảng cách
Ví dụ 1: Cho tọa độ Oxyz trong không gian, đường thẳng d:x=2+4t;y=3=2t và z=−3+t. Mặt phẳng (P):−x+y+2z+5=0. Viết phương trình nằm trong mặt phẳng (P) song song và cách d một khoảng bằng
Giải:
Tổng kết
Qua bài viết tại congthuctoanlyhoa , hy vọng các bạn học sinh đã nắm rõ được kiến thức của phương trình đường thẳng trong không gian cũng như có nền tảng vững về phân môn hình học 12 trong chương trình THPT. Chúc các bạn học tập tốt và đạt được thành tích cao trong kỳ thi THPT QG tới đây.