Hàm số bậc nhất là một phần kiến thức quan trọng trong chương trình toán học đại số lớp 9, hôm nay chúng ta sẽ đi vào tìm hiểu về bài học này. Trước tiên hãy cùng congthuctoanlyhoa nhắc lại một chút lý thuyết cũ về phần hàm số.
Nhắc lại lý thuyết về hàm số
Hàm số là gì
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x (x gọi là biến số)
+) Giá trị của hàm số f(x) tại điểm x0 được kí hiệu là f(x0)
+) Tập xác định D của hàm số f(x) là tập hợp các giá trị của x sao cho f(x) có nghĩa.
+) Khi x thay đổi mà y luôn nhận một giá trị không đổi thì ta gọi hàm số y=f(x) được gọi là hàm hằng.
Đồ thị hàm số
Đồ thị hàm số y = f(x) là tập hợp các điểm biểu diễn các cặp giá trị tương ứng (x;f(x)) trên mặt phẳng tọa độ
Hàm số đồng biến, nghịch biến
Cho hàm số y=f(x)y=f(x) xác định trên tập D. Khi đó :
– Hàm số đồng biến trên D ⇔∀x1,x2∈D:x1<x2⇒f(x1)<f(x2)⇔∀x1,x2∈D:x1<x2⇒f(x1)<f(x2)
– Hàm số nghịch biến trên D ⇔∀x1,x2∈D:x1<x2⇒f(x1)>f(x2)
Hàm số bậc nhất là gì
Khái niệm hàm số bậc nhất
Hàm số bậc nhất là hàm số được cho bởi công thức y=ax+b trong đó a,b là các số cho trước và a≠0
Khi b = 0, hàm số có dạng y = ax.
Tính chất
Xét hàm số y = ax + b (a ≠ 0), ta có:
• Với a > 0, hàm số đồng biến trên ℝ.
• Với a < 0, hàm số nghịch biến trên ℝ.
• Đồ thị hàm số đi qua hai điểm A(0; b) và
Từ đó ta lập được bảng biến thiên và vẽ đồ thị hàm số.
Các dạng bài tập thường gặp
Dạng 1: Nhận dạng hàm số bậc nhất
Ví dụ: Cho hàm số y = 2x + 5. Đây có phải là hàm số bậc nhất không?
Phương pháp: Hàm số bậc nhất là hàm số có dạng y = ax + b (a ≠ 0)
Vậy, hàm số y = 2x + 5 là hàm số bậc nhất.
Dạng 2: Tìm m để hàm số đồng biến, nghịch biến
Ví dụ: Cho hàm số y = (m – 1)x + 3. Tìm m để hàm số đồng biến/nghịch biến
Phương pháp:
Hàm số y = ax + b:
– Đồng biến trên R, nếu a > 0;
– Nghịch biến trên R, nếu a < 0.
Vậy, hàm số y = (m – 1)x + 3 đồng biến khi (m – 1) > 0; nghịch biến khi (m – 1) < 0.
Đồ thị của hàm số bậc nhất
Đồ thị của hàm số bậc nhất y = ax + b (a ≠ 0) là một đường thẳng:
– Có hệ số góc là a;
– Cắt trục tung tại điểm có tung độ bằng b;
– Song song với đường thẳng y = ax (nếu b ≠ 0) và trùng với đường thẳng y = ax (nếu b = 0).
Lưu ý:
Đồ thị của hàm số bậc nhất y = ax + b (a ≠ 0) còn được gọi là đường thẳng y = ax + b. b được gọi là tung độ gốc của đường thẳng y = ax + b.
Trong trường hợp a = 0, hàm số suy biến thành y = b, trở thành một hàm hằng, lúc này đồ thị là một đường thẳng song song với trục hoành.
Cách vẽ đồ thị của hàm số y = ax + b (a ≠ 0)
Cho hàm số y = ax + b, ta chọn hai điểm M, N. Vẽ một đường thẳng đi qua hai điểm M(0;b) và N(-b/a;0) ta được đồ thị của hàm số y = ax + b.
Như vậy, ta có các bước vẽ đồ thị của hàm số bậc nhất:
- Bước 1: Chọn hai điểm M, N.
Cho x = 0 thì y = b => ta được điểm M(0;b) thuộc trục tung Oy
Cho y = 0 thì x = -b/a => ta được điểm N thuộc trục hoành Ox.
- Bước 2: Đánh dấu hai điểm vừa chọn trên trục tung và trục hoành
- Bước 3: Vẽ một đường thẳng đi qua hai điểm M, N vừa chọn. Như vậy, ta đã hoàn thành xong đồ thị jcura hàm số bậc nhất y = ax + b (a ≠ 0)
Bài tập liên quan đến đồ thị hàm số bậc nhất
Sau khi tìm hiểu qua lý thuyết về Hàm số bậc nhất trong chương trình Đại số lớp 9, chúng ta sẽ đến với các dạng bài tập liên quan về phần kiến thức quan trọng này
Dạng 1: Vẽ đồ thị hàm số y = ax + b.
Ví dụ: Vẽ đồ thi của hàm số bậc nhất y = 2x.
Phương pháp:
Cho x = 0 thì y = 0, ta được điểm O(0;0) thuộc trục Oy
Cho y = 2 thì y = 1, ta được điểm A(1;2) thuộc trục Ox
Ta có đồ thị hàm số:
Đồ thị hàm số y = 2x
Dạng 2: Tìm tọa độ của một điểm khi biết trước điều kiện
Ví dụ: Tìm tọa độ điểm P trên đồ thị hàm số, biết P là giao điểm của hai đường thẳng y = 2x + 1 và y = x + 1.
Phương pháp:
Vì P là giao điểm của hai đường thẳng nên ta có phương trình:
Suy ra ta có tọa độ điểm P(0;1).
Bài tập tự luyện
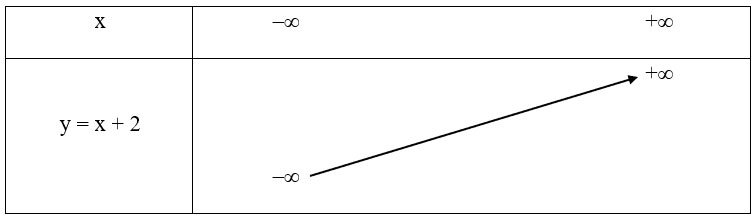
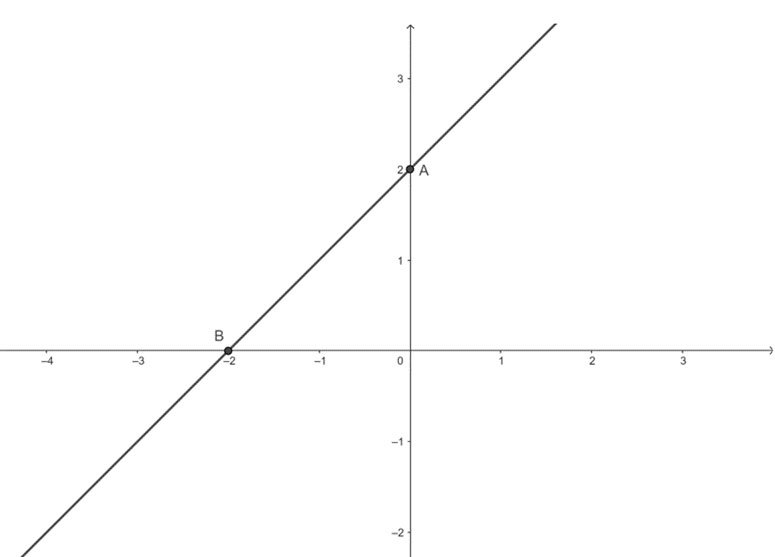
Bài 1. Lập bảng biến thiên và vẽ đồ thị của hàm số y = x + 2.
Hướng dẫn giải:
a = 1 > 0 nên hàm số đồng biến trên ℝ.
Bảng biến thiên:
Đồ thị hàm số đi qua A(0; 2), B(–2; 0).
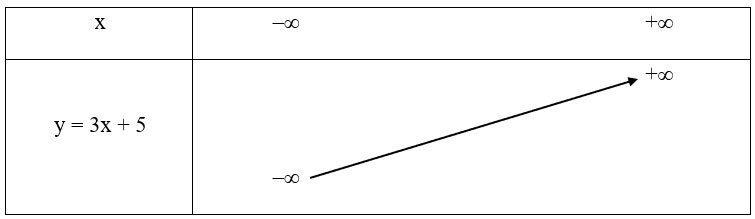
Bài 2. Lập bảng biến thiên và vẽ đồ thị của hàm số y = 3x + 5.
Hướng dẫn giải:
a = 3 > 0 nên hàm số đồng biến trên ℝ.
Bảng biến thiên:
Đồ thị hàm số đi qua A(0; 5), .
Tổng kết
Như vậy, ở trên là hệ thống các kiến thức về hàm số bậc nhất trong chương trình toán học lớp 9, hy vọng Công thức Toán Lý Hóa đã giúp các bạn hiểu hơn về lý thuyết cũng như phương pháp làm bài tập. Chúc các bạn học tập thật tốt và đạt kết quả cao.