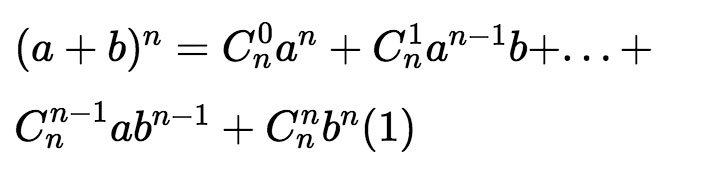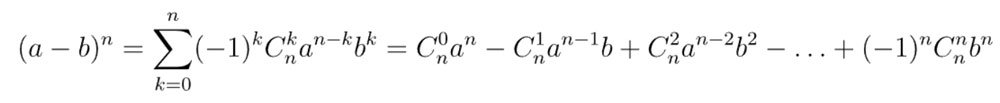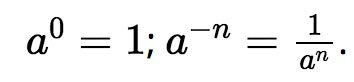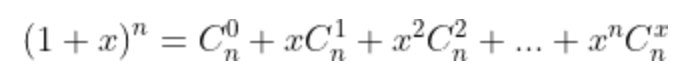[Toán 11] Nhị thức Newton – ĐỦ BỘ lý thuyết và cách giải CỰC CHUẨN

Nhị thức Newton trong chương trình Toán 11 có thể nói là một nội dung khá khó để có thể ghi nhớ. Tuy nhiên, dưới đây là tổng hợp đủ bộ lý thuyết về nhị thức Newton và cách giải cực chuẩn, cùng những mẹo ghi nhớ giúp bạn dễ dàng ghi nhớ về công thức cũng như cách giải các dạng toán liên quan đến phần nội dung này.

Bạn đang đọc bài viết: [Toán 11] Nhị thức Newton – ĐỦ BỘ lý thuyết và cách giải CỰC CHUẨN

Lý thuyết nhị thức Newton

Nhị thức Newton là một công thức triển khai hàm mũ của tổng. Cụ thể là khai triển một nhị thức bậc n ((a + b)ⁿ ) thành một đa thức có n+1 số hạng.

Công thức nhị thức Newton

Với a, b là những số thực tùy ý và với mọi số tự nhiên n ≥ 1, ta có:

Vì vai trò của a và b như nhau nên hoán đổi vị trí a và b ta có công thức tương đương như sau:

Các khai triển nhị thức Newton thường gặp: 

Mẹo ghi nhớ: trong mỗi số hạng thì tổng số mũ của a và b luôn bằng n. Và trong mỗi khai triển có n+1 số hạng

Xem thêm kiến thức về: [Toán 10] Bất đẳng thức Cosi – chuẩn kiến thức và bài giải chi tiết

Tính chất của nhị thức Newton

Công thức nhị thức Newton

• Số các số hạng của công thức là n + 1
• Tổng số mũ của a và b trong mỗi số hạng luôn luôn bằng số mũ của nhị thức:

( n – k) + k = n

• Số mũ của a giảm dần từ n đến 0
• Số mũ của b tăng dần từ 0 đến n
• Số hạng tổng quát của nhị thức là:

T_k+1 = C_n^k a^n-k b^k ( Đó là số hạng thứ k + 1 trong khai triển ( a + b)ⁿ )

• Các hệ số nhị thức cách đều hai số hạng đầu, cuối thì bằng nhau

Hệ quả nhị thức Newton:

• Với a=b=1 thì ta có

Nghĩa là: tổng các hệ số của các số hạng trong sự khai triển của nhị thức bằng 2ⁿ

• Với a=1, b=-1 thì ta có

Nghĩa là: tổng tất cả các hệ số đứng ở vị trí chẵn bằng tổng tất cả các hệ số đứng ở vị trí lẻ

Tam giác Pascal – hệ số của đa thức trong nhị thức Newton

Mô hình tam giác Pascal

Để xây dựng tam giác Pascal, trong hàng 0 (hàng trên cùng), có một số 1 duy nhất. Mỗi số của mỗi hàng tiếp theo được xây dựng bằng cách thêm số ở trên và bên trái với số ở trên và sang bên phải, coi các mục trống là 0. Ví dụ: số ban đầu trong hàng đầu tiên (hoặc bất kỳ số nào khác) là 1 (tổng của 0 và 1), trong khi các số 1 và 3 trong hàng thứ ba được thêm vào để tạo ra số 4 ở hàng thứ tư.

Tính chất của tam giác Pascal

• Mỗi số là tổng của hai số trên nó.
• Các số bên ngoài đều là 1.
• Tam giác là đối xứng.
• Đường chéo đầu tiên hiển thị số đếm.
• Tổng của các hàng có lũy thừa là 2.
• Mỗi hàng cho các chữ số của lũy thừa là 11.
• Mỗi mục nhập là một “chọn số” thích hợp.
• Và đó là “hệ số nhị thức.”

Áp dụng tam giác Pascal vào bài toán nhị thức Newton

Tam giác Pascal xác định các hệ số xuất hiện trong khai triển nhị thức . Nghĩa là hàng thứ n của tam giác Pascal bao gồm các hệ số của biểu thức khai triển của đa thức (x + y) ⁿ .

Khai triển của (x + y) ⁿ  là:

(x + y) ⁿ  = a ₀ x ⁿ  + a ₁ x ^n-1 y + a ₂ x ^n-2 y ²  +… + a _n-1 xy ^n-1  + a _n y ⁿ

trong đó các hệ số dạng a k chính xác là các số trong hàng thứ n của tam giác Pascal.

Ví dụ:

Khai triển biểu thức (x + y) ⁿ  với n = 3.

(x + y) ³  = 3C ₀ x ³  + 3C ₁  x ² y + 3C ₂  xy ²  + 3C ₃  x ⁰ y ³

= (1) x ³  + (3) x ² y + (3) xy ²  + (1) y ³

Ở đây, các hệ số 1, 3, 3, 1 đại diện cho các phần tử ở hàng thứ 3 của tam giác pascal.

Các dạng toán và bài giải về nhị thức Newton

Trong chương trình Đại số 11 thì có các dạng bài tập về nhị thức Newton như sau:

Dạng 1: Tìm hệ số trong khai triển – tìm số hạng trong khai triển

1. Đối với dạng tìm hệ số trong khai triển nhị thức Newton, ta tiến hành như sau:

Bước 1: Sử dụng công thức khai triển nhị thức Newton

Bước 2: Tìm số hạng có chứa x^k và tìm hệ số tương ứng

Ví dụ: Tìm hệ số của x³ trong khai triển ( 2 + x)⁵

Giải:

Ta có

Cho k = 3 ta được hệ số của x³ là: C³₅. 2^5-3 = 40

2. Đối với dạng tìm số hạng trong khai triển nhị thức Newton, ta tiến hành theo các bước sau:

Bước 1: Khai triển nhị thức Newton để tìm số hạng tổng quát:

Bước 2: Dựa vào đề bài, giải phương trình hai số mũ bằng nhau

Số hạng chứa x^m ứng với giá trị k thỏa: np – pk + qk = m

Từ đó tìm: k = ( m – np) / ( p – q)

Vậy hệ số của số hạng chứa x^m là: C_n^k a^n-k b^k với giá trị k đã tìm được ở trên

Nếu k không nguyên hoặc k > n thì trong khai triển không chứa x^m, hệ số phải tìm bằng 0

Chú ý: Xác định hệ số của số hạng chứa x^m trong khai triển

P(x) = ( a + bx^p + cx^q)ⁿ được viết dưới dạng a₀ + a₁x + …+ a_2nx²ⁿ 

Ta làm như sau:

• Viết P (x) = ( a + bx^p + cx^q)ⁿ

• Viết số hạng tổng quát khi khai triển các số hạng dạng bx^p + cx^q
• Thành một đa thức theo lũy thừa của x
• Từ số hạng tổng quát của hai khai triển trên ta tính được hệ số của x^m

Chú ý: Để xác định hệ số lớn nhất trong khai triển nhị thức Newton

Ta làm như sau:

• Tính hệ số a_k theo k và n
• Giải bất phương trình sau với ẩn số k

• Hệ số lớn nhất phải tìm ứng với số tự nhiên k lớn nhất thỏa mãn bất phương trình trên

Ví dụ: Tìm số hạng thứ 21 trong khai triển ( 2 – 3x)²⁵

Giải:     Số hạng thứ 21 trong khai triển là:

          C²⁰₂₅. 2⁵ ( -3x)²⁰ = 2⁵. 3²⁰. C²⁰₂₅. X²⁰

Dạng 2: Bài toán tính tổng, chứng minh đẳng thức

Đối với dạng bài toán tỉnh tổng, chứng minh đẳng thức như này, ta tuần tự tiến hành như sau:

Bước 1: Sử dụng khai triển:

(a + b)ⁿ = C⁰_n aⁿ + C¹_n a^n-1b + C²_n a^n-2b² + …+ C^n-1 _n ab^n-1 + Cⁿ_n bⁿ

Bước 2: Suy ra điều phải chứng minh

Bằng cách thay a, b, n bằng các giá trị thích hợp ta sẽ được các đẳng thức.

Dạng 3: Bài toán ứng dụng nhị thức Newton vào các bài toán tổ hợp

Với dạng toán này, ta tiến hành theo các bước:

Bước 1: Chọ một khai triển ( a+ x)ⁿ phù hợp, ở đây a là hằng số

Bước 2: Sử dụng các phép biến đổi đại số hoặc lấy đạo hàm, tích phân

Bước 3: Dựa vào điều kiện bài toán, thay x bởi một giá trị cụ thể

Tổng kết

Hi vọng thông qua bài tổng hợp kiến thức này , các bạn đã có thể nắm được kiến thức lý thuyết về nhị thức Newton, cũng như các mẹo ghi nhớ, các cách giải đối với từng dạng toán khác nhau. Cùng xem thêm các bài tổng hợp kiến thức bổ ích khác ngay tại congthuctoanlyhoa.com .