Đối với phần Hình học không gian, ta được tìm hiểu về các loại khối trụ, khối chóp, khối nón,…Một trong những phần kiến thức được áp dụng khá nhiều đó chính là công thức thể tích khối trụ trong chương trình Toán học lớp 12. Hôm nay chúng ta cùng tìm hiểu tất tần tật công thức tính thể tích của khối hình này nhé!
Bạn đnag xem bài viết: công thức thể tích khối trụ các loại
Khái niệm khối trụ, thể tích khối trụ
Khối trụ là hình trụ cùng với phần bên trong của hình trụ đó
Thể tích khối trụ là lượng không gian mà hình trụ chiếm.
Xem thêm Kiến thức: [Toán 12]Phương trình đường thẳng trong không gian Mới 2022
Cách vẽ khối trụ
Cho những bạn nào chưa hình dung được cách vẽ khối trụ trong chương trình Hình học lớp 12 có thể tham khảo các bước dưới đây:
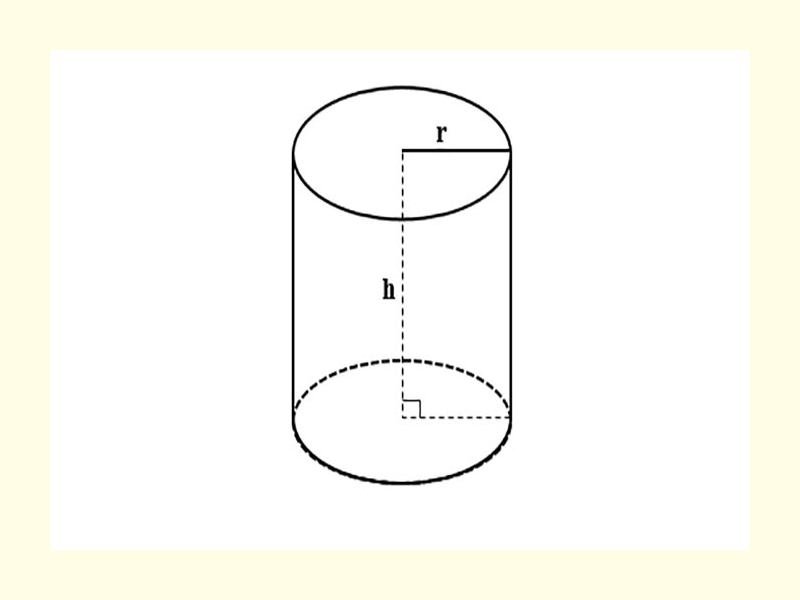
Ta biết hình trụ (khối trụ) là một hình được giới hạn bởi mặt trụ và hai đường tròn có đường kính bằng nhau.
Các bước vẽ khối trụ:
- Ta có một hình chữ nhật ABCD, khi quay hình chữ nhật này quanh một cạnh cố định của chính nó thì ta sẽ có một hình trụ. Vậy ta chọn CD là cạnh cố định
- AB là trục hình trụ, CD là đường sinh hình trụ (AB = CD = h = chiều cao của hình trụ)
- Hình tròn tâm A có bán kính R = AD. Hình tròn tâm B có bán kính R = BC. Hai hình tròn này là hai đáy của hình trụ.
Công thức tính thể tích khối trụ
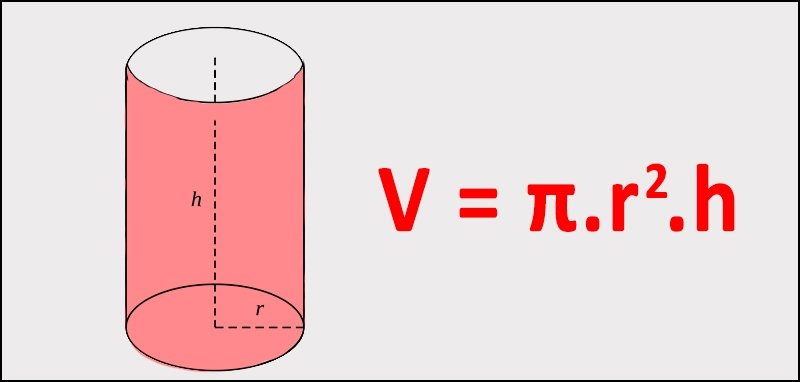
Để tính thể tính khối trụ, ta áp dụng công thức lấy chiều cao nhân với bình phương độ dàu bán kính hình tròn mặt đáy và số pi.
V = π. R2.h
Trong đó:
V: thể tích khối trụ
R: bán kính đáy trụ
h: chiều cao, khoảng cách giữa hai đáy khối trụ.
Đơn vị đo thể tính là mét khối (m3)
Bài tập luyện tập
Bài 1: Tính thể tích của khối trụ biết khoảng cách giữa hai tâm đáy là a(m) và đường kính của đáy là b(m).
Hướng dẫn giải:
2R = B => R = b/2
h = OO’ = a
=> V = π.R2.h = π = (b2/4).a = (ab2/4)π (m3)
Bài 2: Một hình trụ có diện tích xung quanh là 20π cm² và diện tích toàn phần là 28π cm². Tính thể tích của hình trụ đó.
Hướng dẫn giải:
Công thức diện tích toàn phần hình trụ là Stp = Sxq + Sđ = 2πrh + 2πr²
Suy ra, 2πr² = 28π – 20π = 8π
Do đó, r = 2cm
Diện tích xung quanh hình trụ là Sxq = 2πrh
<=> 20π = 2π.2.h
<=> h = 5cm
Vậy ta tính được thể tích hình trụ là V = πr²h = π.22.5 = 20π cm³
Bài 3: Cho hình chữ nhật ABCD có AC = 10cm, AB = 6CM. Cho đường gấp khúc ABCD quay quanh AD ta được hình trụ. Tính thể tích khối trụ được giới hạn bởi hình trụ trên.
Hướng dẫn giải:
Bài 3: Một khối trụ có chu vi đáy bằng 20 dm, diện tích xung quanh bằng 14 dm². Tính chiều cao và thể tích của khối trụ đó.
Hướng dẫn giải
Vì đáy khối trụ là một hình tròn nên chu vi đáy của khối trụ là chu vi của hình tròn = 2rπ = 20 dm
Diện tích xung quanh của khối trụ:
Sxq = 2πrh= 20 x h = 14
=> h = 14/20 = 0,7 (dm)
2rπ = 20 => R ~ 3,18 dm
Vậy thể tích của khối trụ cần tìm: V = π r² x h ~ 219,91 dm³
Tổng kết
Như vậy bài viết vừa rồi của congthuctoanlyhoa.com đã chỉ ra công thức tính thể tích khối trụ mà các bạn đang tìm kiếm. Từ một công thức nhưng chúng ta có thể vận dụng biến đổi linh hoạt để tìm ra đáp án của nhiều bài tập khác nhau nhé! Chúc các bạn học tập thật tốt!
