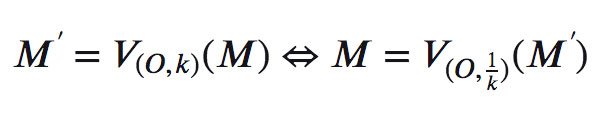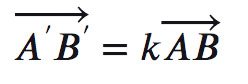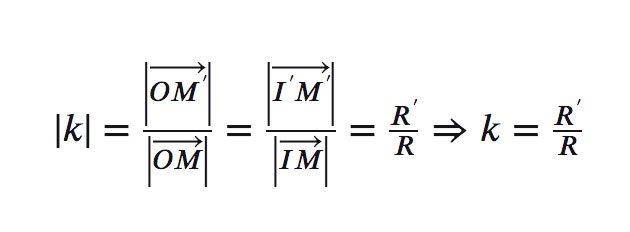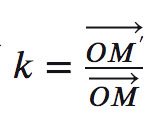Phép vị tự là một trong những dạng quan trọng trong chương trình Hình học 11. Qua bài viết này của congthuctoanlyhoa, các bạn học sinh cố gắng đọc thật kỹ để ghi nhớ lý thuyết và bài tập của dạng bài về phép vị tự này nhé!
Phép vị tự là gì?
Định nghĩa
Cho điểm O và số k≠0. Phép biến hình biến mỗi điểm M thành điểm M’ sao cho vecto , được gọi là phép vị tự tâm O, tỉ số k.
Ký hiệu của phép vị tự tâm O, tỉ số k thường là V(O,k)
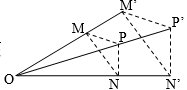
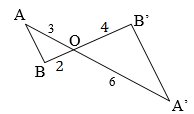
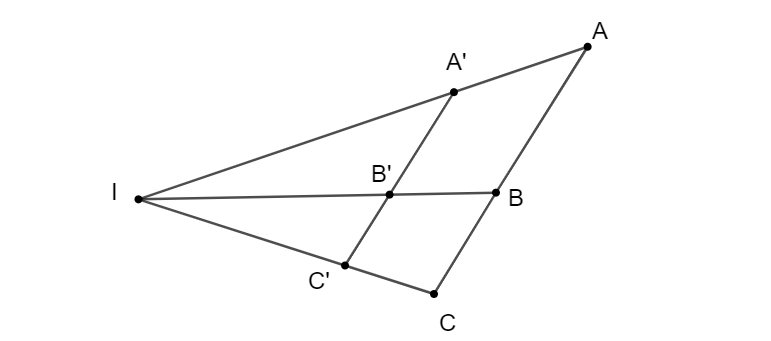
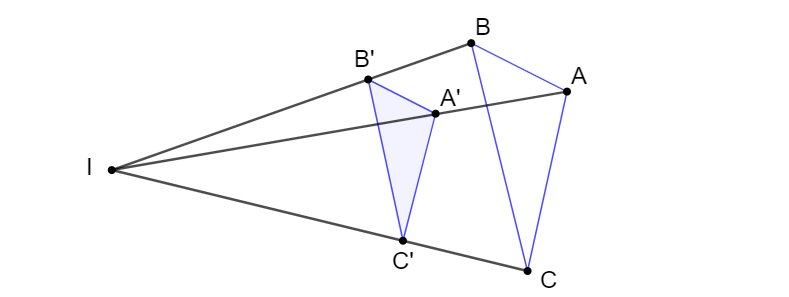
Ví dụ minh hoạ cho phép vị tự:
Nhận xét quan trọng
Trong phép vị tự có một điểm bất động là tâm vị tự.
- Khi k=1 thì phép vị tự V(O;k) là phép đồng nhất
- Khi k=-1 thì phép vị tự V(O;k) chính là phép đối xứng tâm O (khi đó tâm vị tự trở thành tâm đối xứng)
Qua phép vị tự tâm O với tỉ số k biến M thành M’ thì phép vị tự tâm O tỉ số 1/k sẽ biến M’ thành M:
Công thức phép vị tự
Các tính chất phép vị tự
- Với phép vị tâm I, tỉ số k (hay còn gọi là V(I;k)) biến 2 điểm A, B thành A’, B’ thì
- Tính chất khác:
- Từ 3 điểm thẳng hàng cho trước, ta biến 3 điểm đó thành 3 điểm thẳng hàng và thứ tự giữa các điểm vẫn giữ nguyên bảo toàn
- Biến tia thành tia, biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng có độ dài a thành đoạn thẳng có độ dài |k|a
- Biến tam giác thành tam giác đồng dạng có tỉ số đồng dạng là |k|, biến góc thành góc bằng nó
- Phép vị tự có thế biến đường tròn bán kính r thành đường trón bán kính kr.
Tâm vị tự của hai đường tròn
Định lý
Khi cho hai đường tròn bất kỳ, luôn có một phép vị tự biến đường tròn này thành đường tròn kia.
Cách tìm tâm vị tự
Xác định/tìm tâm vị tự của 2 đường tròn (I;R) và (I’;R’)
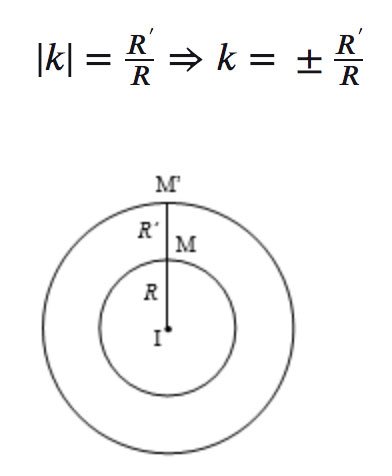
Trường hợp 1: I trùng I’
- Tâm vị tự: Điểm I
- Tỷ số vị tự:
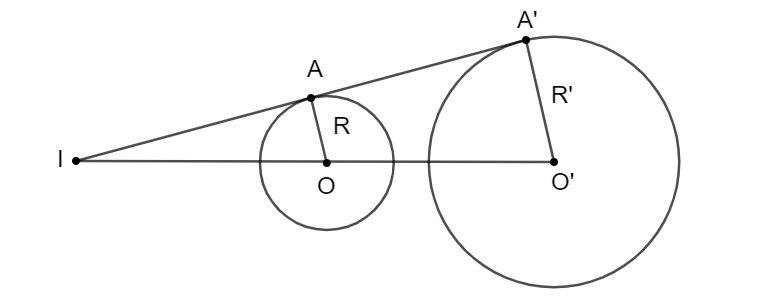
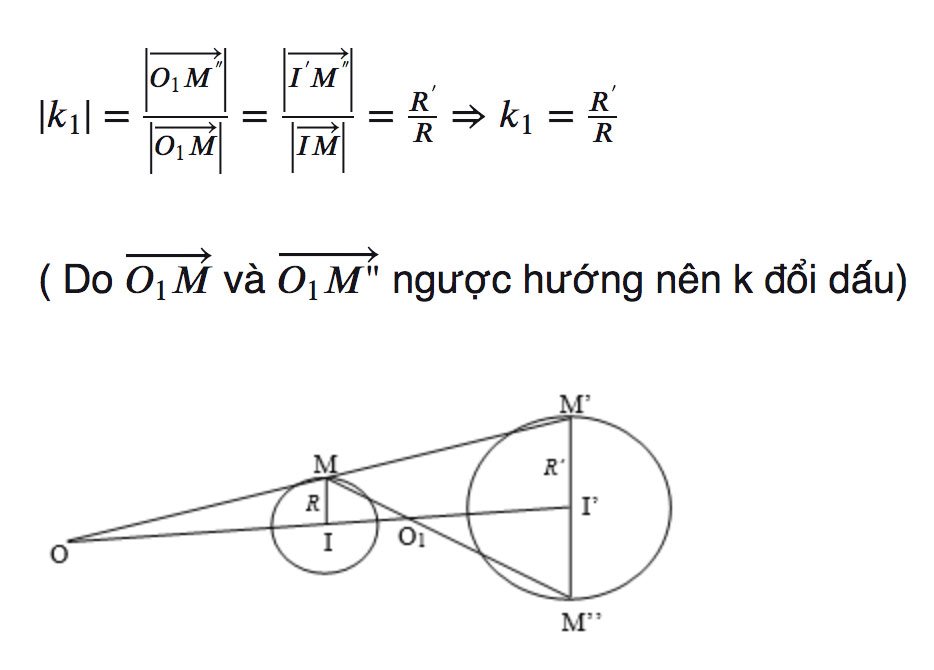
Trường hợp 2: Với I ≠ I’ và R ≠ R’
- Tâm vị tự: O là tâm vị tự ngoài, O1 là tâm vị tự trong
- Tỷ số vị tự
- Với tâm O
(Do OM→ và OM′→ cùng hướng nên k không đổi dấu)
- Với tâm O1
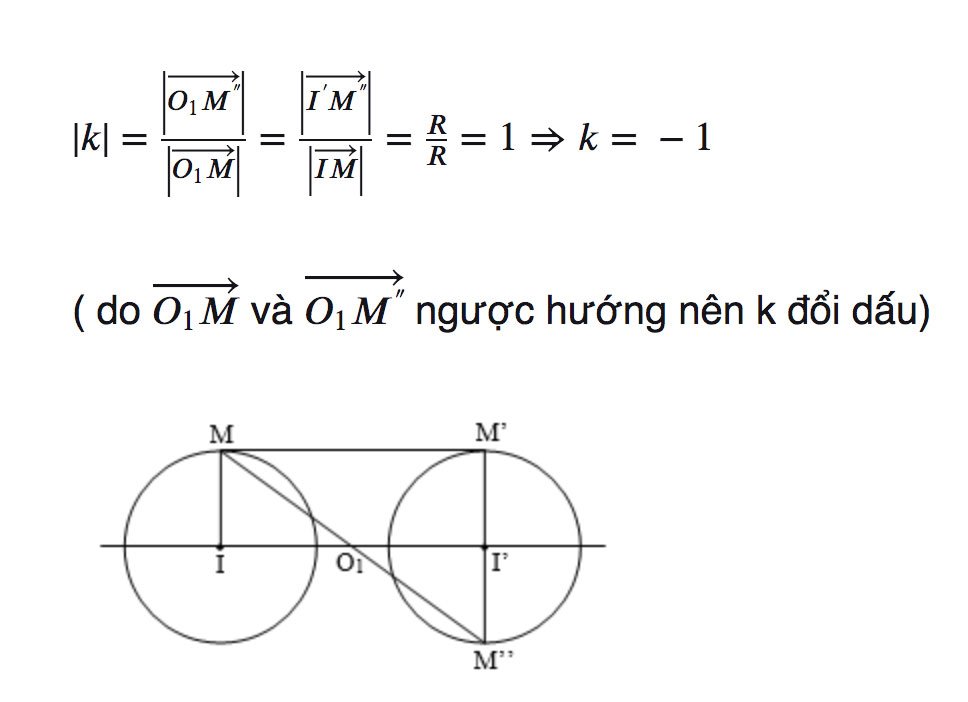
Trường hợp 3: I ≠ I’ và R = R’
- Tâm vị tự: Chính là O1 trên hình vẽ bên dưới
- Tỷ số vị tự
Các dạng bài tập phép vị tự và cách giải
Trong Hình học 11, tương tự như các phép khác, nó cũng sẽ được chia làm các dạng cơ bản sau:
Dạng 1: Tìm các yếu tố của phép vị tự biến điểm M cho sẵn thành điểm M’
- Phương pháp:
Các trường hợp có thể xảy ra:
- TH1: Nếu cho sẵn tâm O, ta tìm tỷ số
- TH2: Nếu cho sẵn k, ta tìm O là điểm chia đoạn MM’ theo tỷ số k
Dạng 2: Sử dụng phép vị tự để xác định tập hợp điểm cần tìm
- Phương pháp: Để tìm tập hợp điểm N cần tìm, ta thực hiện lần lượt theo các bước sau:
- B1: Xác định phép vị tự V(O;k): M → N
- B2: Tìm ra tập hợp điểm H những điểm M, suy ra tập hợp những điểm N là H’, ảnh của H qua phép vị tự V(O;k)
Dạng 3: Dựng hình nhờ phép vị tự
- Phương pháp:
- B1: Tìm phép vị tự biến hình H thành hình H’
- B2: Dựng hình H’ rồi tìm được hình H
Bài tập minh họa
Ví dụ 1: Cho hai đường thẳng cắt nhau d và d’. Tính số phép vị tự biến đường thẳng đó thành chính nó là bao nhiêu?
A. Không có phép nào
B. Có một phép duy nhật
C. Chỉ có hai phép
D. Có vô số phép
Lời giải:
Đáp án D vì tâm vị tự là giao điểm của d và d’. Suy ra có vô số k vậy có vô số phép phép vị tự biến đường thẳng đó thành chính nó
Ví dụ 2: Cho hai đường thẳng d và d’ song song và một điểm O bất kỳ không nằm trên chúng. Số phép vị tự tâm O có thể biến đường thẳng d thành đường thẳng d’?
A. Vô số
B. Chỉ một
C. Chỉ hai
D. Không có
Lời giải:
Đáp án B
Lấy đường thẳng a bất kỳ đi qua O cắt d và d’ lần lượt tại A và A’
Gọi k thoả mãn: số k không phụ thuộc đường thẳng a. Vậy đáp án là phép biến đường thẳng d thành đường thẳng d’ phép vị tự tâm O tỉ số k.
Ví dụ 3: Một hình vuông có S = 4. Qua phép vị tự V(I,−2) thì ảnh của hình vuông trên có S tăng gấp bao nhiêu lần S ban đầu?
A. 2
B. 4
C. 8
D. 1/2
Lời giải:
S=4⇒ cạnh hình vuông bằng 2
V(I;-2) ⇒ cạnh hình vuông mới bằng |-2|. Cạnh hình vuông cũ
⇒ cạnh hình vuông mới bằng 4
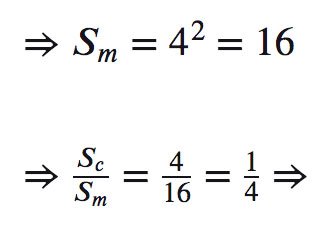
Tổng kết
Bài viết tổng hợp các công thức, bài tập và đáp án về Phép vị tự đến đây là kết thúc. congthuctoanlyhoa mong rằng các bạn qua bài học này đã hiểu và nắm vững hơn về các kiến thức nền cũng như dạng toán của phép này.