Bài viết này congthuctoanlyhoa sẽ giải đáp cho các em về căn bậc 2 là gì? Công thức căn bậc 2 và các dạng toán thường gặp liên quan đến căn bậc 2.
Căn bậc 2 là gì?
Căn bậc hai là kiến thức căn bản và vô cùng quan trọng trong môn toán. Bài viết dưới đây sẽ làm sáng tỏ: căn bậc 2 là gì, cách tính căn bậc 2 và các dạng toán thường gặp.
Căn bậc hai của một số x là một số y sao cho khi bình phương số y thì ta được số x.
Dấu căn được kí hiệu là: √
Ví dụ: 5 và -5 là căn bậc 2 của 25
vì 5² = (-5)² = 25
Tính chất của căn bậc 2
Mọi số dương x đều có căn bậc hai, √x là căn bậc hai dương và -√x là căn bậc hai âm.
Chúng được kí hiệu đồng thời là ±√x
Mọi số thực dương đều có một căn bậc hai không âm duy nhất, được gọi là căn bậc hai số học
Ví dụ:
Số 0 cũng được gọi là căn bậc hai số học của 0
Căn bậc hai của một số âm thuộc về phạm trù số phức. Cụ thể:
Tổn tại một số i gọi là đơn vị ảo, được định nghĩa sao cho i2 = −1. Từ đây ta có thể suy ra i là căn bậc hai của −1, nhưng ta lại có (−i)2 = i2 = −1 do đó −i cũng là căn bậc hai của −1.
Với quy ước này, căn bậc hai của −1 là i, hay tổng quát hơn, nếu x là một số không âm bất kỳ thì căn bậc hai của −x là
Vế phải là căn bậc hai của −x, bởi
Một số căn bậc 2 thường gặp
Việc nhớ nhanh giá trị lũy thừa mũ 2 của một số sẽ khiến quá trình giải toán diễn ra một cách nhanh hơn. Dưới đây là tổng hợp các lũy thừa mũ 2 thường gặp.
0² = 0 6² = 36 12² = 144
1² = 1 7² = 49 13² = 169
2² = 4 8² = 64 14² = 196
3² = 9 9² = 81 15² = 225
4² = 16 10² = 100 12² = 144
5² = 25 11² = 121 16² = 256
Công thức tính căn bậc 2 chuẩn bộ giáo dục
Căn bậc hai xuất hiện trong nhiều dạng toán, dưới đây là tổng hợp các công thức tính căn bậc hai thường gặp. Áp dụng biến đổi linh hoạt khi gặp các dạng toán khác nhau.
Cách tính căn bậc 2 không dùng máy tính
Tính căn bậc 2 bằng cách nhân
Tính căn bậc hai của số x bằng cách tìm một số y nhỏ hơn x, nhẩm tính y nhân y. Làm liên tục cho đến khi được kết quả y nhân y bằng x.
Ví dụ: ta cần tìm căn bậc hai của 30, tìm số nhỏ hơn 30 nên chọn số 5. Nhẩm tính 5×5 là 25, chưa bằng 30 nên tiếp tục tăng giá trị lên và nhẩm. Khi nào số ta chọn thỏa mãn điều kiên y nhân y bằng 30 thì y chính là căn bậc hai của 30.
Tính căn bậc 2 bằng cách tính bắc cầu
Tức là ta sẽ so sánh số cần tìm căn bậc hai với số ta đã biết căn bậc hai trước đó. Tiếp đến tiến hành ước lượng số. Sau khi ước lượng thì lấy số vừa tìm được nhân với chính nó. Làm liên tục cho đến khi được kết quả bằng đúng với số cần tìm căn bậc hai.
Ví dụ: ta cần tìm căn bậc hai của 70, ta đã biết trước căn bậc hai của 64 là 8. Và căn bậc hai của 81 là 9, tức là căn bậc hai của 70 nằm giữa 8 và 9. Ta chọn một số x trong khoảng này, rồi nhân x với chính nó cho đến khi có kết quả x nhân x bằng 70.
Nếu có thể thì hãy sử dụng máy tính trong các trường hợp tìm căn bậc hai không phải số lập phương để có thể có kết quả chính xác nhất nhé.
Các dạng toán có các căn bậc 2 thường gặp
Trong chương trình Đại số 9 thì thường gặp các dạng toán căn bậc hai như sau:
Dạng 1: Tìm điều kiện của biến để biểu thức có nghĩa
Phương pháp: áp dụng quy tắc √B có nghĩa khi B lớn hơn hoặc bằng 0 và 1/√B có nghĩa khi B lớn hơn 0. Sau đó giải bất phương trình để biểu thức có nghĩa.
Dạng 2: Rút gọn biểu thức chứa căn thức
Để rút gọn các biểu thức chứa căn cần vận dụng các phép toán như: đưa thừa số ra ngoài dấu căn, vào trong dấu căn, trục căn thức ở mẫu, sử dụng hằng đẳng thức để phân tích thành nhân tử và tìm mẫu thức chung,…
Ví dụ:
Cho K = 2(1√x−1−1√x):(√x+1x2−x)2(1x−1−1x):(x+1×2−x) (với x>0;x≠1x>0;x≠1). Rút gọn biểu thức K.
Bài giải:
K = 2(1√x−1−1√x):(√x+1x2−x)
=2[√x−√x+1(√x−1)√x]:√x+1x(√x−1)(√x+1)2(1x−1−1x):(x+1×2−x)
=2[x−x+1(x−1)x]:x+1x(x−1)(x+1)
=2√x.(√x−1):1x(√x−1)
=2√x
Dạng 3: Giải phương trình có chứa căn thức
Để làm dạng này ta áp dụng các định nghĩa về điều kiện của biểu thức trong căn hoặc đưa về dạng phương trình có dấu giá trị tuyệt đối.
Một số bài toán minh họa về căn bậc 2
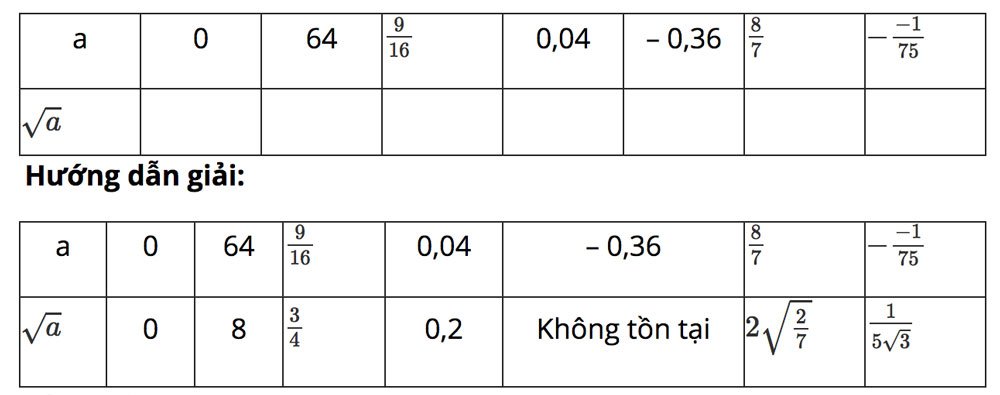
Bài 1. Tìm các căn bậc hai số học của các số sau:
Bài 2. Tính

Bài 3. So sánh:
a) 3 và
b) 5 và
Hướng dẫn giải:
a) Vì 9 < 11 nên . Vậy 3 < b) Vì 25 > 5 nên . Vậy 5 > .
Bài 4. Chứng minh.
Tổng kết
Thông qua bài viết về căn bậc 2 và cách tính căn bậc 2 theo chuẩn bộ giáo dục đã trình bày ở trên, congthuctoanlyhoa.com hi vọng đã có thể giúp các em nắm được nội dung kiến thức về căn bậc hai, giải tốt các bài tập thuộc dạng này và cả các dạng toán liên quan của chương trình học nữa.