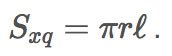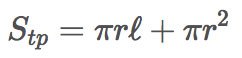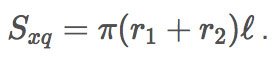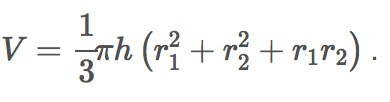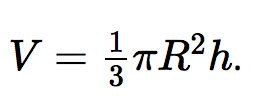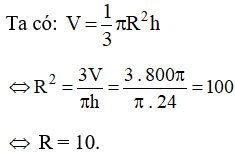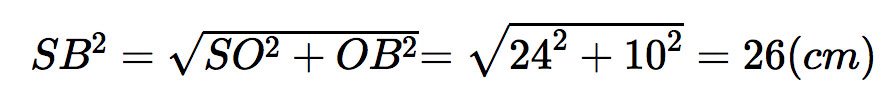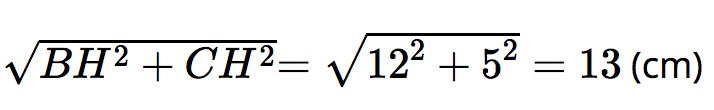Bài viết hôm nay congthuctoanlyhoa sẽ truyền tải về kiến thức của hai hình học khác nhau: Hình nón và Hình nón cụt. Tuy không khó nhưng các bạn học sinh cần tập trung và luyện tập nhiều để nhuần nhuyễn các công thức dưới đây.
Hình nón là gì?
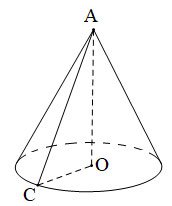
Khi quay một tam giác vuông AOC vòng quanh cạnh OA, ta được một hình nón. Khi đó:
- Cạnh OC tạo nên đáy của hình nón là một đường tròn tâm O, bán kính OC
- Cạnh AC quét nên một mặt xung quanh của hình nón AC, gọi là đường sinh
Diện tích xung quanh hình nón
Diện tích toàn phần hình nón
Thể tích hình nón
Hình nón cụt là gì?
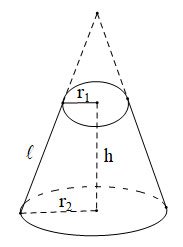
Khi cắt hình nón bởi một mặt phẳng song song với mặt đáy, ta được một hình nón cụt.
Diện tích xung quanh
Thể tích hình nón cụt
Các dạng bài tập
Tìm bán kính, đường sinh, diện tích, thể tích hình nón
Lời giải
Cho hình nón có chiều cao là h, bán kính đáy R và đường sinh là l thì có:
- Diện tích xung quanh: Sxq = πRl
- Diện tích đáy (hình tròn): Sđ = πR2
- Diện tích toàn phần hình tròn: S = Sđ + Sxq = π.r.l+πr2
- Thể tích khối nón:
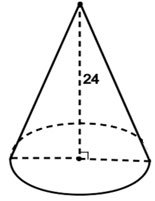
Ví dụ: Một hình nón có đường cao bằng 24 cm và thể tích bằng 800π cm3. Tính diện tích toàn phần của hình nón này.
Lời giải:
Gọi R là bán kính và h là chiều cao của hình nón.
Do đó bán kính của hình nón là 10 cm.
Đường sinh của hình nón là:
Diện tích toàn phần của hình nón là:
Stp = πR(l + R) = π . 10 (26 + 10) = 360π (cm2).
Bài tập minh họa hình nón và hình nón cụt
Bài 1:
Cách xác định thiết diện hình nón
Lời giải
Nếu cắt mặt nón tròn xoay bởi mặt phẳng đi qua đỉnh, thì có các trường hợp sau xảy ra:
- Mặt phẳng cắt mặt nón theo 2 đường sinh thì thiết diện là tam giác cân.
- Mặt phẳng tiếp xúc với mặt nón theo một đường sinh, trong trường hợp này, người ta gọi đó là mặt phẳng tiếp diện của mặt nón.
Nếu cắt mặt nón tròn xoay bởi mặt phẳng không đi qua đỉnh, thì có các trường hợp sau xảy ra:
- Mặt phẳng cắt vuông góc với trục hình nón thì giao tuyến là một đường tròn.
- Mặt phẳng cắt song song với 2 đường sinh hình nón thì giao tuyến là 2 nhánh của 1 hypebol.
- Mặt phẳng cắt song song với 1 đường sinh hình nón thì giao tuyến là 1 đường parabol.
Bài tập minh họa
Bài 1: Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều cạnh 2a. Tính diện tích xung quanh của hình nón.
Hướng dẫn:
Cắt hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là tam giác SAB, ∆SAB đều cạnh 2a.
Sxq = πRl = π.a.2a = 2πa2
Bài 2:
Tính diện tích xung quanh, diện tích toàn phần hình nón, tính thể tích khối nón
Lời giải
Cho hình nón (H) có bán kính đường tròn đáy là R và độ dài đường sinh là l.
- Diện tích xung quanh hình nón bằng nửa tích số của độ dài đường tròn đáy và độ dài đường sinh: Sxq = πRl
- Diện tích toàn phần của hình nón bằng tổng diện tích xung quanh và diện đáy: Stp = πR.l + πR2
- Thể tích khối nón bằng một phần ba tích số diện tích hình tròn đáy và chiều cao:
Bài tập minh họa
Một hình nón đỉnh S có bán kính đáy bằng 9 cm và chiều cao SO = 21,6 cm. Cắt hình nón bởi một mặt phẳng song song với đáy tạo ra một hình nón cụt có chiều cao 12 cm. Tính diện tích xung quanh của hình nón cụt.
Lời giải:
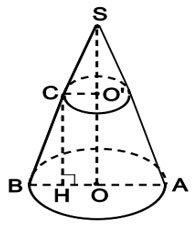
Xét mặt cắt qua trục của hình nón là ∆SAB cân tại S.
Trong mặt phẳng SAB có O’C // OB.
Trong mặt phẳng SAB vẽ , ta được:
CH = OO’ = 12 cm, BH = 9 – 4 = 5 (cm).
Suy ra BC =
Diện tích xung quanh của hình nón cụt là:
Sxq = π(R1 + R2)l = π(9 + 4) . 13 = 169π (cm2)
Vậy diện tích xung quanh của hình nón cụt là 169π cm2.
Tổng kết
Bài viết tại congthuctoanlyhoa đã tổng hợp các kiến thức tổng quát nhất kèm theo bài giải chi tiết cho các dạng toán về diện tích hình nón và hình nón cụt. Các bạn học sinh hãy nhớ rèn luyện thật nhiều để có thể thuộc lòng tất cả các công thức quan trọng trên khi làm bài nhé!