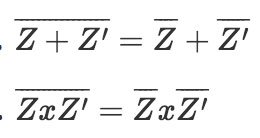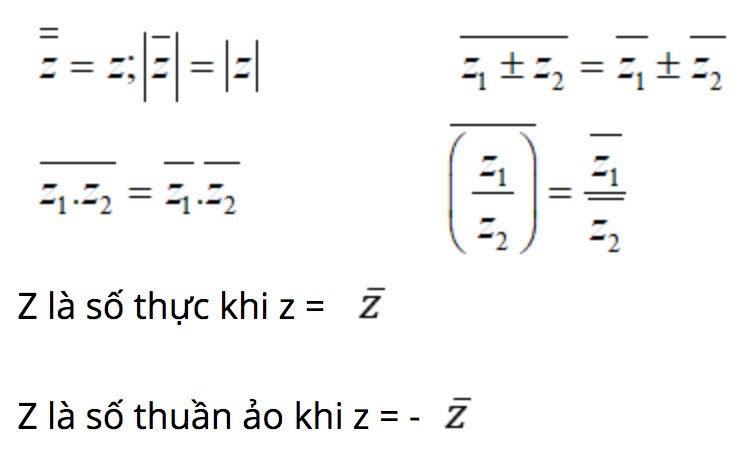Số phức là gì?
Định nghĩa
- Số phức là số có dạng z = a + bi, trong đó a và b là các số thực, còn i là đơn vị ảo với i2 = -1.
- Trong biểu thức này, a được gọi là phần thực, b gọi là phần ảo, còn i là đơn vị ảo.
- Tập hợp các số phức kí hiệu là C. Với dạng biểu thức C= {a + bi; a, b ∈ R và i2 = -1}. Như vậy ta có R⊂C.
- Số phức có phần ảo bằng 0 là một số thực: z = a + 0.i = a∈R⊂C
- Số phức có phần thực bằng 0 là một số ảo: z = 0.a + bi = bi. Đặc biệt i = 0 + 1.
- Số 0 = 0 + 0.i vừa là số thực vừa là số ảo.
- Số phức trong tiếng Anh là complex number. Vì thế nó mới có ký hiệu là C.
Sự khác biệt giữa số phức và số thực
Từ định nghĩa ta có thể thấy rằng số phức là trường hợp tổng quát hơn của số thực. Số thực là 1 trường hợp cụ thể của số phức (khi b = 0). Để dễ hình dung nhất, ta tiến hành so sánh và minh họa cụ thể chúng trong không gian 2 chiều như sau.
Như hình minh họa trên, trục x (trục hoành) biểu diễn cho phần thực, còn trục y (trục tung) biểu diễn cho phần ảo. Những con số thực mà ta tính toán trước kia sẽ giống như r3, r5 được biểu diễn như trên hình trong không gian phức.
Tìm hiểu thêm về số thực để thấy rõ sự khác biệt giữa số phức và số thực.
Số phức liên hợp, số phức thuần ảo, số thuần thực
1. Số phức liên hợp
Theo như định nghĩa ở trên, số phức có dạng a + bi với i2 = -1.
- Số phức liên hợp chính là a-bi và được ký hiệu là
¯z , với ¯z = a-bi
Ví dụ: ta có z= 2+3i, vậy số phức liên hợp của z là ¯z 2-3i
- Các tính chất của số phức liên hợp
∣z∣=∣z∣;∀z∈C
Do đó 2 điểm biểu diễn của z và ¯z sẽ đối xứng với nhau qua trục Oxy trên mặt phẳng tọa độ Oxy.
Theo công thức này, liên hợp của một tổng sẽ bằng tổng các số phức liên hợp. Công thức trên còn đúng với cả phép trừ, phép nhân và phép chia.
z¯z = a2 + b2
Đây là công thức quan trọng và thường được áp dụng nhiều trong các bài toán.
- Cách tìm số phức liên hợp
Cho số phức z = a + bi. Ta gọi số phức liên hợp của số phức z = a + bi là ¯z=a-bi
Kết quả: ∀ z ∈ C ta có:
2. Số phức thuần ảo
Khi phần thực a=0 thì Z= bi thuộc R. Khi đó Z là số thuần ảo.
3. Số thuần thực
Khi phần ảo b=0 thì Z=a thuộc R. Khi đó Z là số thuần thực ( hay số thực)
Số được gọi là vừa là số thuần thực vừa là số thuần ảo khi số 0 = 0 + 0i.
Các dạng toán liên quan đến số phức
Trong chương trình Toán 12, có các dạng toán liên quan đến số phức như sau:
Dạng bài tập biến đổi số phức
Dạng toán về tính toán liên quan đến số phức như cộng, trừ, nhân, chia, liên hợp, mô đun.
Nếu như không có tham số thì chúng ta có thể sử dụng máy tính bỏ túi để tính.
Còn nếu như bài toán có chứa tham số. Thì chúng ta vận dụng đúng định nghĩa các phép toán cộng, trừ, nhân, chia, liên hợp, mô đun số phức để biến đổi.
1. Dạng bài tạp liên quan đến số thực và số ảo
Số thực là số có phần ảo bằng 0 và ngược lại số ảo (thuần ảo) là số có phần thực bằng 0.
2. Dạng bài tập liên quan đến 2 số phức bằng nhau
Hai số phức bằng nhau khi và chỉ khi phần thực bằng phần thực, đồng thời phần ảo bằng phần ảo.
3. Các bài tập tìm phần thực hoặc phần ảo của số phức
Ta biến đổi số phức đã cho thành z=a+bi, trong đó a và b là các số thực. Khi đó a là phần thực của z, còn b là phần ảo của z. Chú ý các bài toán về số phức mà hỏi về phần ảo người ta hay có phương án nhiễu bi. Nên cẩn thận chú ý phần này.
4. Dạng bài tập tìm số phức liên hợp
Số phức liên hợp của a+bi (với a và b là các số thực) là a-bi. Tức là chúng ta chỉ cần đổi dấu phần ảo để được số phức liên hợp của số phức đã cho.
5. Dạng bài tập tìm mô-đun số phức
Với số phức z=a+bi, trong đó a và b là các số thực thì mô đun của z là căn bậc 2 không âm của a²+b².
6. Dạng bài tập số phức mũ cao
Cách tính số phức mũ cao là sử dụng dạng lượng giác hoặc dạng mũ của số phức.
Với số phức dạng e mũ ta áp dụng công thức sau:
Các dạng bài tập số phức liên quan đến nghiệm phương trình
1. Bài tập giải phương trình chứa z và số phức liên hợp của z
Phương pháp giải
Cho số phức z = a + bi. Ta gọi số phức liên hợp của z là 
Kết quả: ∀ z ∈ C ta có:
2. Bài tập chứa z và mô-đun của z
Đối với dạng toán này, nếu giả sử z=a+bi xong thay vào giải hệ thì thường sẽ được một hệ phức tạp. Vì vậy trước tiên ta cứ giả sử z=a+bi xong thay vào phương trình xem liệu có giải được hệ đó không. Nếu thấy khó khăn ta thử xoay sang hướng rút z và lấy mô đun 2 vế để được phương trình hệ quả. Phương trình này sẽ tìm được mô đun của z. Sau đó ta lấy mô đun của z thay vào phương trình ban đầu và giải tiếp.
3. Các dạng bài tập số phức liên quan đến phương trình bậc 2 với hệ số thực
Với phương trình bậc 2 hệ số thực trên tập số phức ta chia làm 2 nhóm: Nhóm các bài tập liên quan đến việc tìm nghiệm và nhóm các bài tập liên quan đến định lý Viet.
Thông thường với phương trình không có tham số ta sử dụng máy tính bỏ túi có thể cho ra kết quả ngay. Còn nếu có tham số thì ta tính Delta và thay vào công thức nghiệm hoặc sử dụng định lý Viét.
Tổng kết
Bài viết trên là bài viết tổng hợp lại toàn bộ kiến thức về lý thuyết lẫn bài tập vận dụng của liên quan đến số phức. Hi vọng thông qua bài viết, congthuctoanlyhoa.com đã có thể giúp bạn củng cố kiến thức, tự tin chinh phục các đề thi.