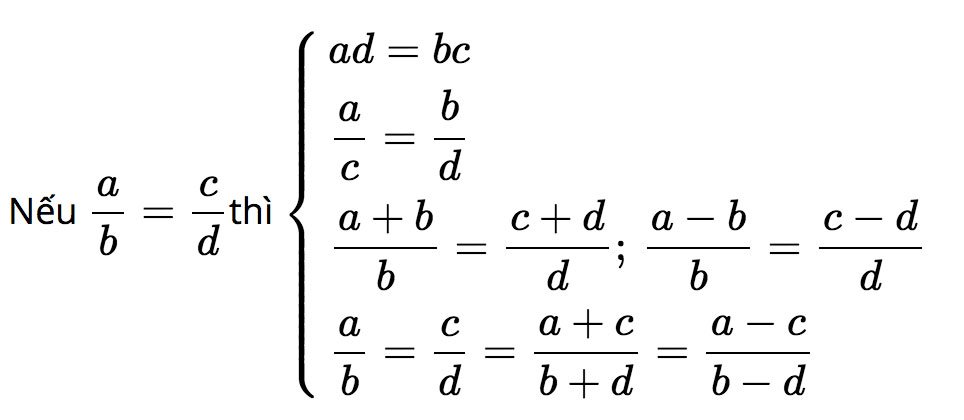Đây là bài mở đầu cho Chương 3: Tam Giác Đồng Dạng trong phân môn hình học lớp 8. Trong bài viết, congthuctoanlyhoa sẽ giới thiệu đến các bạn các kiến thức về Định lý Talet (cả trong tam giác và hình thang), định lý Talet đảo và hệ quả của nó. Ngoài ra, một số bài tập ứng dụng kèm lời giải chi tiết sẽ giúp các bạn hiểu rõ hơn về bài học lần này.
Tỉ số của hai đoạn thẳng
Tỉ số của hai đoạn thẳng
Tỉ sổ của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
Tỉ số của hai đoạn thẳng không phụ thuộc vào cách chọn đơn vị đo
Tỉ số của hai đoạn thẳng không phụ thuộc vào cách chọn đơn vị đo
Ví dụ: Cho đoạn thẳng AB và một tỉ số m/n>0. Điểm C thuộc AB biết CA/CB=m/n. Khi đó, ta gọi điểm C là điểm chia đoạn thẳng AB theo tỉ số m/n.
Đoạn thẳng tỉ lệ
Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng và nếu có tỉ lệ thức:
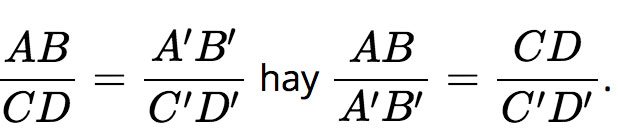
Định lý Talet trong hình học
Trong tam giác
Định lý Talet trong tam giác là một định lý căn bản trong chương trình Hình học 8. Nó được dùng để chứng minh các vấn đề trong tam giác của hình học phẳng.
Định lý thuận
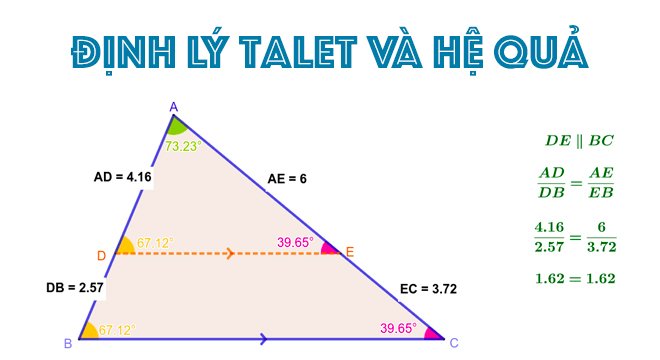
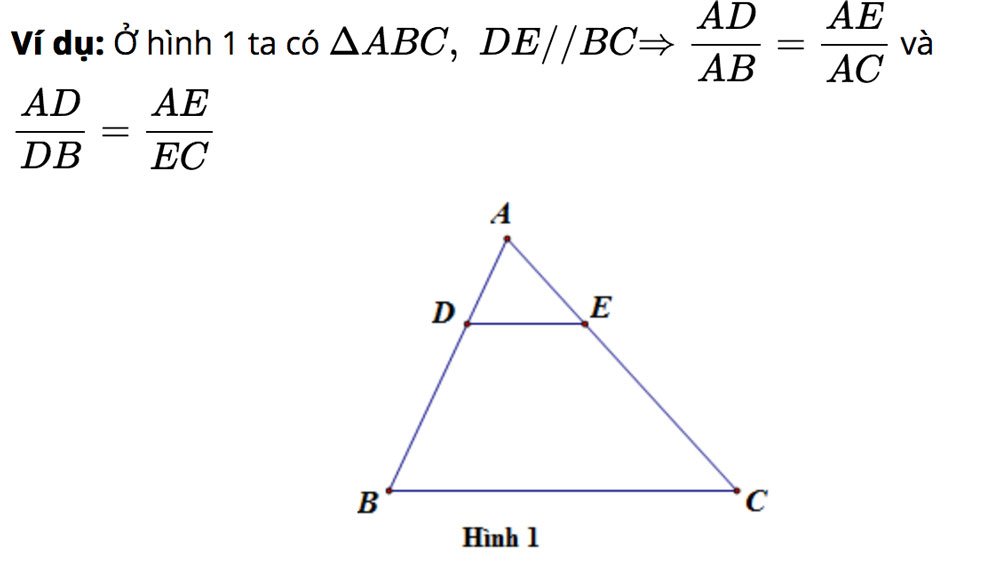
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Định lý đảo
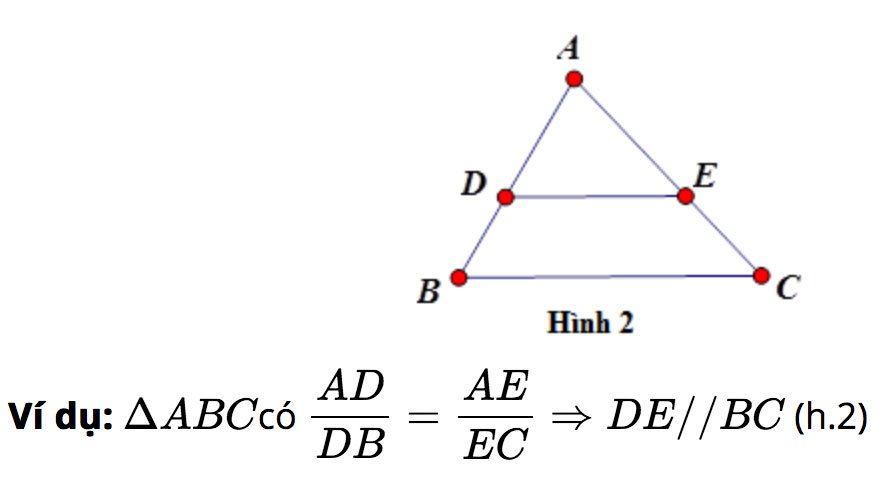
Nếu một đường thẳng cắt hai cạnh của tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Hệ quả
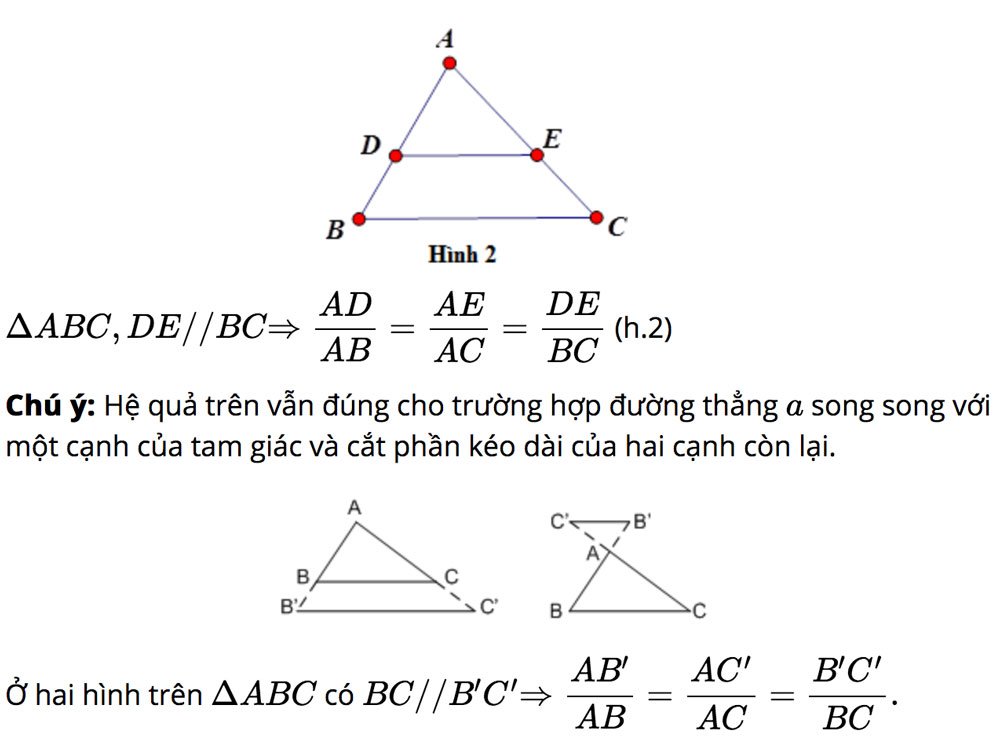
Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Trong không gian
Dạng 1. Tính độ dài của đoạn thẳng, chu vi và diện tích, các tỉ số
Phương pháp:
Để giải các bài toán dạng này, ta sử dụng định lý Talet, hệ quả của định lý Talet và tỉ số đoạn thẳng để tính toán.
+ Định lý: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
+ Hệ quả: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh tam giác đã cho.
+ Ngoài ra, ta còn sử dụng đến tính chất tỉ lệ thức:
Dạng 2: Chứng minh hai đường thẳng song song và chứng minh đẳng thức hình học
Để giải các bài toán thuộc dạng này, chúng ta sẽ sử dụng định lý Talet, định lý Talet đảo và hệ quả của định lý Talet để chứng minh.
Định lý Talet tổng quát
Định lý thuận
Định lý thuận sẽ được phát biểu như sau:
Nếu có một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó sẽ định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Định lý đảo
Định lý đảo sẽ được phát biểu như sau:
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Lưu ý: Định lý vẫn đúng cho trường hợp đường thẳng cắt phần kéo dài hai cạnh của tam giác.
Hệ quả (các đường thẳng đồng quy cắt hai đường thẳng song song)
Được phát biểu như sau:
- Hệ quả 1: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có 3 cạnh tương ứng tỉ lệ với 3 cạnh tam giác đã cho
- Hệ quả 2: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì sẽ tạo ra một tam giác mới đồng dạng với tam giác ban đầu
- Hệ quả 3 – Talet mở rộng: Nếu 3 đường thẳng đồng quy thì chắn trên hai đường thẳng song song các cặp đoạn thẳng tương ứng tỉ lệ
Tổng kết
Bài viết trên đã hệ thống lại các lý thuyết và cách giải cho bài học Định lý Talet. congthuctoanlyhoa mong rằng kiến thức này sẽ giúp cho các bạn học sinh chinh phục được kết quả mong muốn trong học tập, đặc biệt với phân môn Hình học 8 này.