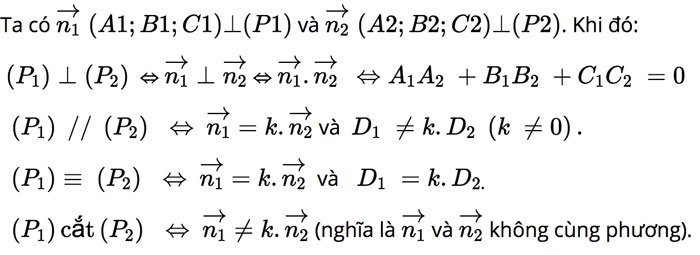Phương trình mặt phẳng là một trong các dạng phương trình căn bản ở chương trình Toán 12. Bài viết này congthuctoanlyhoa.com sẽ mang đến khái niệm về 2 loại vecto quan trọng, cũng như một số kiến thức căn bản khác cùng bài tập và lời giải chi tiết, giúp các bạn học sinh nắm được bài học này.
Vectơ pháp tuyến (VTPT) và Vectơ chỉ phương (VTCP) của hai mặt phẳng
Để hiểu hơn về VTPT, ta có:
(P) là một mặt phẳng trong không gian, 1 vectơ khác vectơ 0 có phương vuông góc với (P) thì được gọi là VTPT của mặt phẳng (P).
Để hiểu hơn về VTCP, ta có:
(P) là một mặt phẳng trong không gian. Khi 2 vectơ khác vectơ 0 và không cùng phương thì gọi là cặp VTCP của (P) nếu giá của chúng nằm song song hoặc nằm trên (P).
* Mặt phẳng hoàn toàn được xác định khi biết một điểm và một vectơ pháp tuyến của nó, hay một điểm thuộc mặt phẳng và cặp vectơ chỉ phương của nó.
Tích có hướng của hai vectơ
Phương trình tổng quát của mặt phẳng
Định nghĩa
Phương trình Ax + By + Cz + D = 0, trong đó A2+B2+C2 ≠ 0, được gọi là phương trình tổng quát của mặt phẳng
Nhận xét
a) Ax + By + Cz + D = 0 ⇒ (P) có 1 VTPT n=(A;B;C)
b) PT của (P) qua M0=(x0;y0;z0) và có VTPT n=(A;B;C) là: A(x-x0) + B(y-y0) + C(z-z0) = 0
Ví dụ 1:Cho mặt phẳng (P) có phương trình 2x+3y-z+2=0. Tìm một vecto pháp tuyến của mặt phẳng.
Giải
Một VTPT của (P) là n=(2;3;-1)
Ví dụ 2:Viết phương trình mặt phẳng đi qua điểm M0=(1;-2;3) và có VTPT n=(-2;1;4)
Giải
Phương trình mặt phẳng (P) qua M0=(1;-2;3) và có VTPT n=(-2;1;4) là:
-2(x-1)+1(y+2)+4(z-4)=0 ⇔ -2x+y+4z-12=0
Viết phương trình mặt phẳng khi biết vectơ pháp tuyến và một điểm thuộc mặt phẳng đó
Phương trình mặt phẳng đi qua điểm M (xo ;yo ;zo ) và có Vecto pháp tuyến (A;B;C) là:
A(x -xo ) +B(y -yo ) +C(z -zo )=0
Vị trí tương đối giữa các mặt phẳng
Cho hai mặt phẳng và có phương trình :
Khoảng cách từ một điểm đến một mặt phẳng
Trong không gian cho mặt phẳng có phương trình:
và điểm .Khoảng cách từ M0 đến được cho bởi công thức:
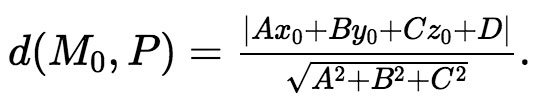
Các dạng bài tập phương trình mặt phẳng
Như các bài học khác trong Hình học 12, phương trình đường thẳng cũng được chia làm các dạng cơ bản.
Viết phương trình mặt phẳng trung trực của đoạn thẳng
Phương pháp: Giả sử (P) là mặt phẳng trung trực của đoanh AB. Ta xác định yếu tố điểm mà (P) đi qua chính là trung điểm AB. Còn vecto pháp tuyến chính là vecto AB.
Ví dụ:
Trong không gian Oxyz, cho điểm A(2;1;3) và điểm B(4;-2;3). Viết phương tri`nh mặt phẳng (P) là mặt phẳng trung trực của đoạn thẳng AB.
Viết phương trình mặt phẳng đi qua 3 điểm cho trước
Phương pháp: Giả sử mặt phẳng (P) đi qua 3 điểm không thẳng hàng A, B, C. Chúng ta có tới tận 3 yếu tố điểm là điểm A, điểm B, điểm C. Thỏa mái để lựa chọn nhưng ta chỉ chọn 1 điểm thôi nhé. Để tìm yếu tố véc tơ pháp tuyến chúng ta lấy tích có hướng của véc tơ AB và véc tơ AC.
Ví dụ:
Trong không gian Oxyz, cho điểm A(2;-2;3), điểm B(0;-2;4) và điểm C(4;1;3). Viết phương trình mặt phẳng (ABC).
Viết phương trình mặt phẳng đi qua 1 điểm vuông góc với 2 mặt phẳng cho trước
Phương pháp: Giả sử ta cần viết phương trình mặt (R) đi qua điểm A và vuông góc với (P), (Q). Yếu tố điểm đã có là điểm A. Yếu tố véc tơ pháp tuyến chính là tích có hướng hai véc tơ pháp tuyến của (P) và (Q).
Ví dụ:
Trong không gian Oxyz, cho điểm A(1;2;3) và các mặt phẳng (P):x+y+z-3=0, (Q): 2x-y+3z-1=0. Viết phương trình mặt phẳng (R) đi qua A vuông góc với mặt phẳng (P) và (Q).
Viết phương trình mặt phẳng đi qua 1 điểm vuông góc với đường thẳng cho trước
Phương pháp: Giả sử ta cần viết phương trình mp(P) đi qua điểm A và vuông góc với đường thẳng d. Yếu tố điểm đã có là điểm A. Yếu tố véc tơ pháp tuyến của mặt phẳng (P) chính là véc tơ chỉ phương của đường thẳng d.
Tổng kết
Bài viết tại congthuctoanlyhoa.com đã tổng hợp đầy đủ các lý thuyết, công thức kèm bài tập minh họa có đầy đủ lời giải về phương trình mặt phẳng cho các bạn. Hy vọng nó sẽ giúp ích và hỗ trợ các bạn học sinh ôn tập và nắm được kiến thức thật vững vàng.