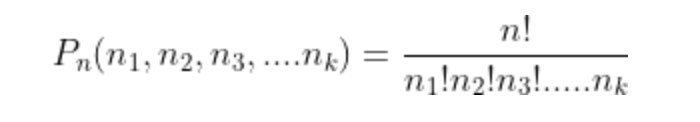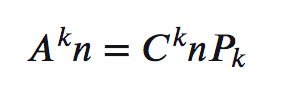[Toán 10] Hoán vị, chỉnh hợp, tổ hợp đầy đủ 8 công thức

Kiến thức về hoán vị – chỉnh hợp – tổ hợp không những là phần cực kì quan trọng trong chương trình Toán 11, mà đây còn là tiền đề cho môn giải tích giải tích và đại số ở chương trình đại học, cao đẳng. Biết được sự quan trọng này, bài viết sau đây đã tổng hợp toàn bộ công thức, cách làm, các dạng toán liên quan đến phần kiến thức này.

Bạn đang đọc bài viết: [Toán 11] Tổng hợp ĐẦY ĐỦ NHẤT 8 công thức hoán vị – chỉnh hợp – tổ hợp

Công thức hoán vị

Khái niệm

Hoán vị được hiểu là một song ánh từ một tập hợp hữu hạn X vào chính nó. Nó diễn tả ý tưởng rằng các đối tượng phân biệt có thể được sắp xếp theo một thứ tự khác nhau.

Theo định nghĩa: Cho tập hợp A gồm n phần tử (n ≥ 1). Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A thì được gọi là một hoán vị của n phần tử đó.

Công thức

Hoán vị không lặp

Định lí: Số các hoán vị của n phần tử khác nhau đã cho được kí hiệu là và:

${{P}_{n}}=n!=1.2.3...n$

Ví dụ: Cho tập A = {1,2,3,4}. Từ tập A có thể lập được bao nhiêu số gồm 4 chữ số phân biệt?

Hướng dẫn: Cho số tự nhiên có 4 chữ số khác nhau nên chữ số đầu tiên có 4 cách chọn, chữ số thứ 2 có 3 cách chọn, chữ số thứ 3 có 2 cách chọn, chữ số cuối cùng có 1 cách chọn. Vậy số các số được tạo thành là: số.

Hoán vị lặp

Cho n phần tử, trong đó có k giá trị khác nhau. Giá trị thứ nhất xuất hiện lần, giá trị thứ 2 xuất hiện lần,…, giá trị thứ k xuất hiện lần sao cho ${{n}_{1}}+{{n}_{2}}+{{n}_{3}}+...+{{n}_{k}}={{n}_{n}}$

Khi đó, số lượng các hoán vị lặp của n phần tử này là:

Ví dụ: Từ các chữ số 0, 1, 2, 3, 4 có thể lập được bao nhiêu số gồm 7 chữ số, trong đó chữ số 2 có mặt 3 lần, các chữ số còn lại có mặt đúng một lần. Xếp các chữ số 0, 1, 2, 3, 2, 3, 4 thành một hàng có gì cách xếp. Xếp các chữ số 0, 1, 2, 3, 2, 3, 4 thành một hàng sao cho chữ số 0 đứng đầu có 9 cách xếp. và 7! 6! i = 1440 số thỏa mãn yêu cầu.

Hoán vị vòng quanh

Mỗi cách sắp xếp n phần tử của A tạo thành một vòng khép kín theo một thứ tự nào đó thìđược gọi là hoán vị vòng quanh của n phần tử. Ở đây ta phân biệt thứ tự theo chiều kim đồng hồ và ngựơc chiều kim đồng hồ và không phân biệt điểm bắt đầu của vòng này.

Kí hiệu:

Công thức tính:

Ví dụ: Có bao nhiêu cách sắp xếp 5 bạn nữ và 3 bạn nam thành 1 vòng tròn sao cho mỗi bạn nam phải đứng giữa bạn 2 nữ bất kỳ?

Chọn 1 bạn nữ cố định, ta xếp 4 bạn nữ còn lại quanh vòng tròn thì giữa 5 bạn nữ này có 5 chỗ trống. Chỉ cần đặt 3 bạn nam vào 3 trong 5 vị trí này thì được ngay một cách xếp. Khi đó, có 4!. A = 1440 cách.

Xem thêm kiến thức quan trọng [Toán 11] Nhị thức Newton – ĐỦ BỘ LÝ THUYẾT VÀ CÁCH GIẢI CỰC CHUẨN

Công thức chỉnh hợp

Khái niệm

Chỉnh hợp là cách chọn lựa các phần tử từ một nhóm lớn hơn và có phân biệt theo thứ tự sắp xếp, trái ngược so với tổ hợp là không phân biệt theo thứ tự sắp xếp.

Theo định nghĩa, chỉnh hợp chập k của n phần tử chính là một tập con của tập hợp mẹ S chứa n phần tử, tập con gồm k phần tử riêng thuộc S, có sắp xếp theo thứ tự.

Công thức

Số chỉnh hợp

Định lí: Số chỉnh hợp chập k của n phần tử khác nhau đã cho được kí hiệu là

$A_{n}^{k}=nleft( n-1 right)left( n-2 right)...left( n-k+1 right)=frac{n!}{left( n-k right)!},left( 1le kle n right)$

Công thức trên cũng đúng cho trường hợp k=0 hoặc k=n

Ví dụ: Có bao nhiêu cách sắp xếp 5 bạn An, Minh, Tâm, Chi, Liên, Đạt vào 8 chiếc ghế trong lớp?

Hướng dẫn: Mỗi cách chọn ra 5 chỗ ngồi vào 8 chiếc ghế đã có sự sắp xếp Có hoán vị là chỉnh hợp chập 5 của 8 $Rightarrow$ Ta có số cách chọn là: cách

Chỉnh hợp lặp

Một dãy bao gồm k phần tử của tập A, trong đó mỗi phần tử có thể được lặp lại nhiều lần, sắp xếp theo một thứ tự nhất định được gọi là một chỉnh hợp lặp chập k của n phần tử.

Ví dụ: với tập A = {1, 2, 3}, các chỉnh hợp lặp chập 2 của A sẽ là: {11}, {12}, {13}, {21}, {22}, {23}, {31}, {32}, {33} .

Số lượng các chỉnh hợp lặp chập k của n phần tử sẽ là:

Ví dụ:

1. Xếp ngẫu nhiên 5 quyển sách vào 3 ngăn kéo. Hỏi có bao nhiêu cách sắp xếp thỏa mãn điều kiện trên?

Mỗi cách sắp xếp 5 quyển sách vào 3 ngăn kéo xem như một chỉnh hợp lặp chập 3 của 5 (mỗi lần xếp một quyển sách vào một ngăn, ta có thể xem như chọn một trong 3 ngăn nên có 3 cách chọn. Do có 5 quyển sách nên số cách chọn là n = 3⁵ = 243 cách.

2. Mỗi vé số của mỗi tỉnh gồm có 6 chữ số. Hỏi mỗi tỉnh khi phát hành mỗi đợt sẽ phát hành được bao nhiêu vé số khác nhau?

Ta có mỗi vé số gồm có 6 chữ số, nên ta có thể xem việc phát hành ra một vé số là việc chọn ra 6 số bất kỳ có thứ tự có thể trùng nhau từ 10 số từ 0 đến 9. Do đó mỗi vé số được phát hành có thể được xem là một chỉnh hợp lặp chập 6 của 10.
Vậy số vé số có thể phát hành mỗi đợt của mỗi tỉnh là số chỉnh hợp lặp chập 6 của 10

Công thức tổ hợp

Khái niệm

Tổ hợp là cách chọn lựa những phần tử từ một nhóm lớn hơn mà không phân biệt thứ tự. Hoặc tổ hợp chập k của n phần tử chính là một tập con của tập hợp mẹ S chứa n phần tử. Phần tử con này gồm k phần tử riêng biệt thuộc S và không sắp xếp theo đúng thứ tự.

Theo định nghĩa: Cho n phần tử khác nhau . Mỗi tập con gồm k phần tử khác nhau của tập hợp n phần tử đã cho được gọi là tổ hợp chập k của n phần tử đã cho.

Công thức

Số tổ hợp

Định lí: Số các tổ hợp chập k của n phần tử khác nhau đã cho kí hiệu là và bằng:

$C_{n}^{k}=frac{n!}{k!left( n-k right)!}, 0le kle n$

Ví dụ: Một nhóm bạn gồm 5 bạn nam và 3 bạn nữ. Hỏi có bao nhiêu cách chọn ra 3 người sao cho có ít nhất 1 người là nam?

Hướng dẫn:

Cách 1:

Có 1 nam, 2 nữ : cách
Có 2 nam, 1 nữ : cách
Có 3 nam, không có nữ: cách

Vậy có tất cả 15 + 30 + 10 = 55 cách

Cách 2:

Số cách chọn 3 người từ 8 người là cách
Số cách chọn sao cho có 3 nữ, 0 nam là: cách

Vậy số cách chọn sao cho có ít nhất 1 bạn nam trong nhóm là 56 – 1 = 55 cách.

Tổ hợp lặp

Một dãy gồm k phần tử của A, trong đó mỗi phần tử có thể lặp lại nhiều lần không tính đến thứ tự sắp xếp của chúng được gọi là một tổ hợp lặp chập k của n phần tử.

Công thức: }

Tổng hợp các dạng toán

Trong chương trình Đại số 11 , về phần nội dung này thì có các dạng bài toán liên quan thường gặp như sau:

Dạng 1: Bài toán đếm

Đối với dạng bài toán đếm như thế này, ta có phương pháp giải đối với riêng từng trường hợp như sau:

Phương pháp giải:

1. Để nhận diện một bài toán đếm có sử dụng hoán vị của n phần tử, ta dựa trên các dấu hiệu như sau:

Tất cả n phần tử đều có mặt
Mỗi phần tử đều chỉ xuất hiện một lần
Có phân biệt giữa các phần tử

2. Để nhận dạng một bài toán đếm có sử dụng chỉnh hợp chập k của n phần tử, ta thường dựa trên các dấu hiệu sau:

Phải chọn k phần tử cho n phần tử trước
Có phân biệt thứ tự giữa k phần tử được chọn

3. Để nhận dạng một bài toán đếm có sử dụng tổ hợp chập k của n phần tử, ta thường dựa trên các dấu hiệu:

Phải chọn k phần tử từ n phần tử cho trước
Không phân biệt thứ tự giữa k phần tử được chọn

Ví dụ:

Với sáu chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên gồm bốn chữ số khác nhau và trong mỗi số nhất thiết phải có chữ số 1?

Hướng dẫn:

Gọi số có 4 chữ số thỏa mãn là abcd

+ Trường hợp 1. Nếu a = 1. Với mỗi cách chọn bcd là một chỉnh hợp chập 3 của 5 phần tử. Nên số cách chọn bcd:

= 60 số

+ Trường hợp 2. Nếu b = 1. Có 4 cách chọn a; có

=12 cách chọn c và d.

⇒ có: 1. 4. 12= 48 số.

+ Tương tự; nếu c= 1; d= 1 cũng có 48 số thỏa mãn.

Suy ra số các số thỏa mãn đầu bài là: 60 + 48 + 48 + 48= 204 số.

Dạng 2: Chứng minh đẳng thức, bất đẳng thức

Đối với dạng toán chứng minh đẳng thức và bất đẳng thức, ta có phương pháp giải sau đây:

Phương pháp giải

Thường sử dụng các cách sau đây

Cách 1: Dùng phép biến đổi

Cách 2: Đánh giá về bất đẳng thức

Cách 3: Chứng minh quy nạp

Cách 4: Dùng phương pháp đếm

Trong phần này, chúng ta chủ yếu sử dụng 3 công thức sau đây:

Dạng 3: Giải phương trình, hệ phương trình, bất phương trình

Đới với dạng bài toán giải phương trình, hệ phương trình và bất phương trình như thế này, ta thường sử dụng một trong hai cách sau đây:

Cách 1: Thực hiện việc đơn giản biểu thức để di chuyển phương tình về dạng đại số quen thuộc

Cách 2: Đánh giá thông qua giá trị cận trên hoặc cận dưới

Tổng kết

Trên đây là toàn bộ bài viết tổng hợp những kiến thức trong chương trình đại số lớp 11, về phần định nghĩa, công thức, các dạng toán cũng như cách giải toán liên quan đến nội dung hoán vị, chỉnh hợp, tổ hợp. Congthuctoanlyhoa.com hi vọng có thể giúp bạn củng cố kiến thức, hiểu, ghi nhớ và giải quyết thật tốt dạng bài tập này.