Một trong những phần quan trọng nhất chính là các hệ thức lượng trong tam giác vuông được áp dụng trong các bài tập Hình học. Hôm nay, chúng ta sẽ cùng tìm hiểu kỹ hơn về phần lý thuyết này và một số bài tập kèm theo.
Một số hệ thức về cạnh và đường cao trong tam giác vuông
Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
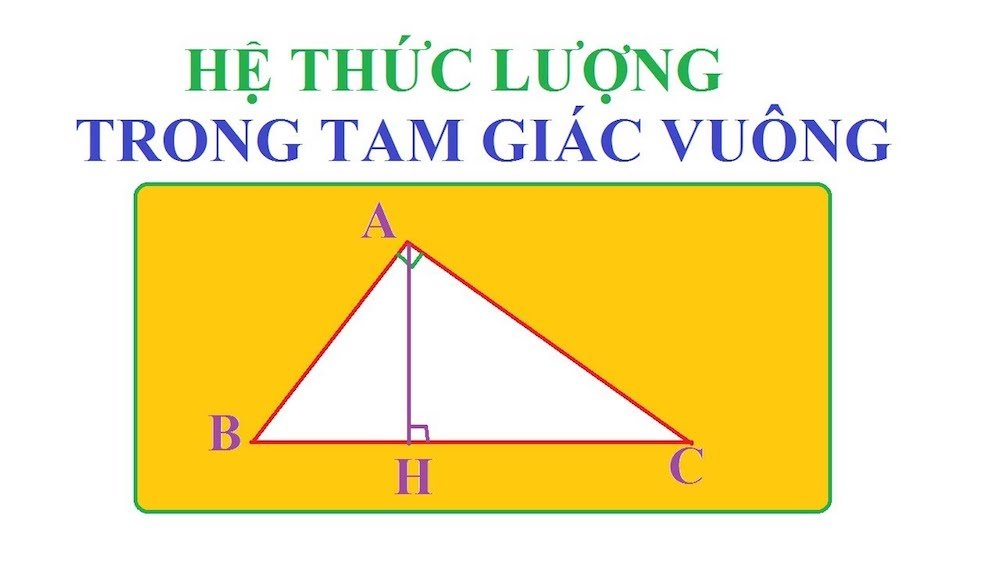
Cho tam giác ABC vuông tại A, ta có định lý sau:
– Các hệ thức liên quan đến hệ thức lượng trong tam giác vuông:
- AB2 = BH * BC
- AC2 = CH * BC
- AH2 = BH * CH
- AB * AC = AH * BC
- 1/AH2 = 1/AB2 * 1/AC2
- Cạnh huyền trong tam giác bình phương bằng tổng bình phương của hai cạnh góc vuông trong tam giác đó.
Định lý 1: Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
b2= a.b’ , c2 = a.c’
Một số hệ thức liên quan đến đường cao trong tam giác vuông
Đối với đường cao trong tam giác ABC vuông tại A, ta cần ghi nhớ các định lý tiếp theo:
Định lý 2: Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
h2 = b’.c’
Định lý 3: Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.
b.c = a.h
Định lý 4: Trong một tam giác vuông, nghịch đảo của bình phương đường cao tương ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.
Lưu ý: Trong các bài tập tính toán, các số đo độ dài ở mỗi bài nếu không hi đơn vị được quy ước là cùng đơn vị đo.
Tỉ số lượng giác của góc nhọn
Khái niệm tỉ số lượng giác của góc nhọn
Định nghĩa về tỉ số lượng giác
- Sinα = Đối / Huyền
- Cosα = Kề / Huyền
- Tanα = Đối / Kề
- Cotα = Kề / Đối
Lưu ý:
- Các tỉ số lượng giác của một góc nhọn luôn luôn dương.
- sin < 1, cos < 1
- Các tỉ số chỉ thay đổi khi độ lớn của góc nhọn đang xét thay đổi
Tỉ số lượng giác của hai góc phụ nhau
Ta có định lý cần nhớ: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tan góc này bằng cot góc kia.
Ta có bảng tỉ số lượng giác các góc đặc biệt
Lưu ý: Khi viết các tỉ số lượng giác của một góc nhọn trong tam giác bất kỳ, ta bỏ ký hiệu “^”. Thay vì viết cos Â, ta sẽ đổi thành cos A
Ta có các công thức dựa trên tỉ số lượng giác của một góc nhọn như sau:
a) Cho α,β là hai góc nhọn. Nếu α < β thì
* sinα < sinβ; tanα < tanβ
*cosα > cosβ; cotα > cotβ
b) sinα < tanα; cosα < cotα
Cách dùng bảng lượng giác để làm bài tập
Sau đây sẽ là cách dùng bảng lượng giác mà các bạn có thể áp dụng để làm bài tập nhé
a. Tìm tỉ số lượng giác của một góc nhọn cho trước
- Bước 1: Tra số độ ở cột 1 đối với sin và tan (cột 13 đối với cos và cot)
- Bước 2: Tra số phút ở hàng 1 đối với sin và tan (hàng cuối đối với cos và cot)
- Bước 3: Lấy giá trị là giao hàng ghi số độ và cột ghi số phút.
b. Tìm số đo của một góc nhọn có tỉ số lượng giác của góc đó
Để có được số đo góc cần tìm, ta cần tra giá trị của tỉ số lượng giác với bảng thích hợp sau đó dóng sang cột độ và hàng phút tương ứng với tỉ số.
Một số hệ thức về cạnh và góc trong tam giác vuông
Cho tam giác ABC vuông tại A có BC=a,AC=b,AB=c.
Ta có :
b=a.sinB=a.cosC; c=a.sinC=a.cosB;
b=c.tanB=c.cotC; c=b.tanC=b.cotB.
Trong một tam giác vuông
+) Cạnh góc vuông =(cạnh huyền ) ×(sin góc đối) = (cạnh huyền ) ×(cosin góc kề)
+) Cạnh góc vuông =(cạnh góc vuông còn lại ) ×(tan góc đối)
= (cạnh góc vuông còn lại ) × (cot góc kề).
Chú ý:
Trong một tam giác vuông nếu cho trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và không kể góc vuông) thì ta sẽ tìm được các yếu tố còn lại.
Tổng kết
Như vậy, bài viết vừa rồi đã điểm qua Hệ thức lượng trong tam giác vuông. Hy vọng các bạn đã hiểu hơn về chương Hình học quan trọng này với sự tổng hợp kiến thức của congthuctoanlyhoa . Đừng quên hãy luyện tập thật nhiều để ghi nhớ nhé.