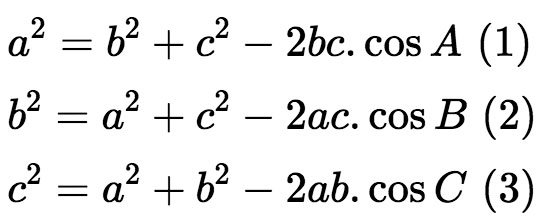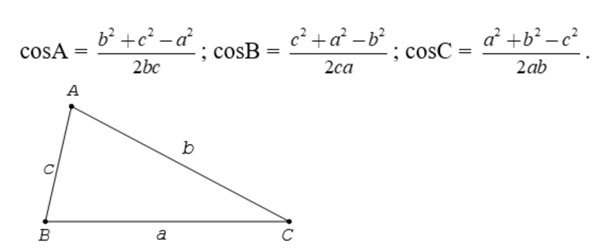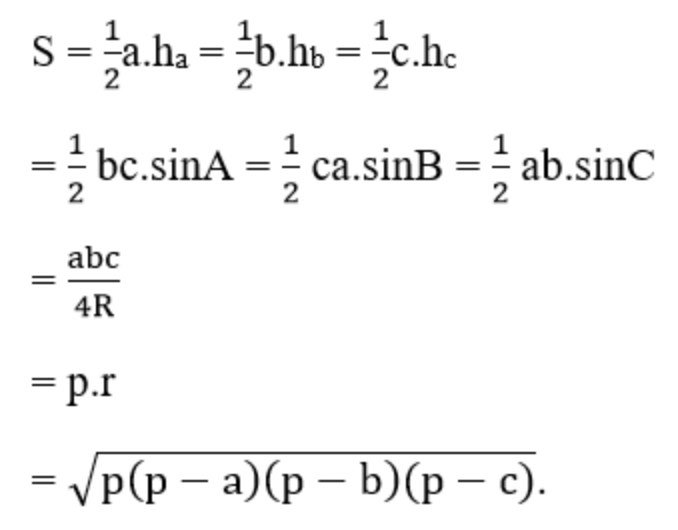Ở lớp 9, ta đã học qua các hệ thức lượng trong tam giác vuông. Trong chương trình lớp 10, ta sẽ lần nữa gặp lại Hệ thức lượng trong tam giác thường, liệu nó có điểm gì khác so với kiến thức trước đây, và thế nào là giải tam giác?
Định lý Cosin trong tam giác
Trong một tam giác bất kỳ, bình phương một cạnh bằng tổng bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng.
Chứng minh ngắn gọn theo tích vô hướng của hai vectơ ở bài học trước, ta có được luận điểm trên.
Như vậy, ta có phát biểu về định lý cosin trong tam giác như sau:
Trong tam giác ABC, gọi Ab = c; AC = b; BC = a, ta có:
Từ đó, ta có hệ quả như sau:
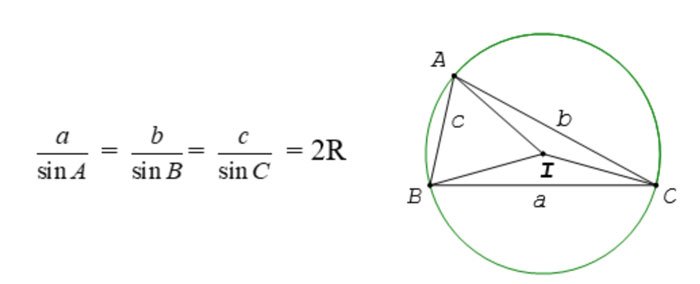
Định lý Sin trong tam giác
Trong tam giác ABC bất kì, tỉ số giữa cạnh và sin của góc đối diện với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác.
Tổng bình phương hai cạnh và độ dài đường trung tuyến của tam giác
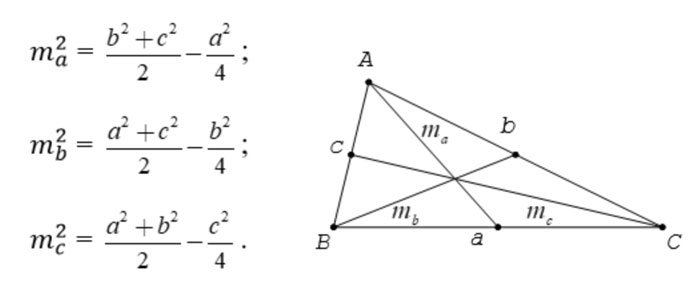
Cho tam giác ABC có ma, mb, mc lần lượt là các trung tuyến kẻ từ A, B, C.
Ta có:
Công thức tính diện tích tam giác
Ngoài kiến thức diện tích từ lớp dưới là bằng nửa tích cạnh đáy nhân với chiều cao tương ứng, trong Hình học 10 này, ta sẽ biết thêm được các công thức sau:
Cho tam giác ABC có:
+) ha, hb, hc là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB;
+) R là bán kính đường tròn ngoại tiếp tam giác;
+) r là bán kính đường tròn nội tiếp tam giác;
+) p = 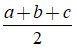
+) S là diện tích tam giác.
Khi đó ta có:
Giải tam giác là gì và ứng dụng thực tế của nó?
Có thể hiểu, giải tam giác là khi ta tính độ dài các cạnh và số đo các góc của tam giác dựa trên điều kiện cho trước.
Muốn giải tam giác, ta cần tìm mối liên hệ giữa các yếu tố đã cho với các yếu tố chưa biết của tam giác thông qua các hệ thức đã được nêu trong định lý cosin, định lý sin và các công thức tính diện tích tam giác.
Các dạng toán hệ thức lượng trong tam giác
Với hệ thức trong tam giác thường và giải tam giác, ta có 4 dạng bài tập cơ bản như sau
Xác định các yếu tố trong tam giác
Phương pháp:
- Sử dụng định lý cosin và định lý sin.
- Sử dụng công thức xác định độ dài đường trung tuyến và mối liên hệ của các yếu tố trong tam giác
Giải tam giác
Có 3 dạng cơ bản như sau:
- Giải tam giác khi biết một cạnh và hai góc ⇒ dùng định lý sin để tính cạnh còn lại
- Giải tam giác khi biết hai cạnh và góc xen giữa ⇒ dùng định lý cosin để tính cạnh thứ ba
- Giải tam giác khi biết ba cạnh ⇒ dùng định lý cosin để tính góc
Chứng minh đẳng thức, bất đẳng thức liên quan đến các yếu tố của tam giác, tứ giác.
Phương pháp:
Sử dụng các hệ thức cơ bản, bất đẳng thức cạnh trong tam giác để biến đổi vế này thành vế kia, hai vế cùng bằng một vế hoặc biến đổi tương đương về một đẳng thức đúng.
Nhận dạng tam giác
Phương pháp:
Sử dụng định lý cosin, sin, công thức đường trung tuyến, công thức tính diện tích tam giác để biến đổi giả thiết về hệ thức liên hệ cạnh (hoặc góc), từ đó suy ra dạng tam giác.
Tổng kết
Trong bài viết này, congthuctoanlyhoa.com gửi đến bạn hệ thống cơ bản về các hệ thức lượng trong tam giác thường và trả lời chi tiết câu hỏi giải tam giác là gì cùng các phương pháp chi tiết cho từng bài giải. Hy vọng các bạn học sinh thấy bài viết hữu ích và áp dụng vào việc học tập của mình.