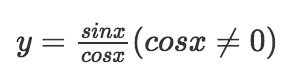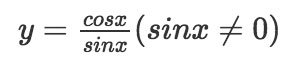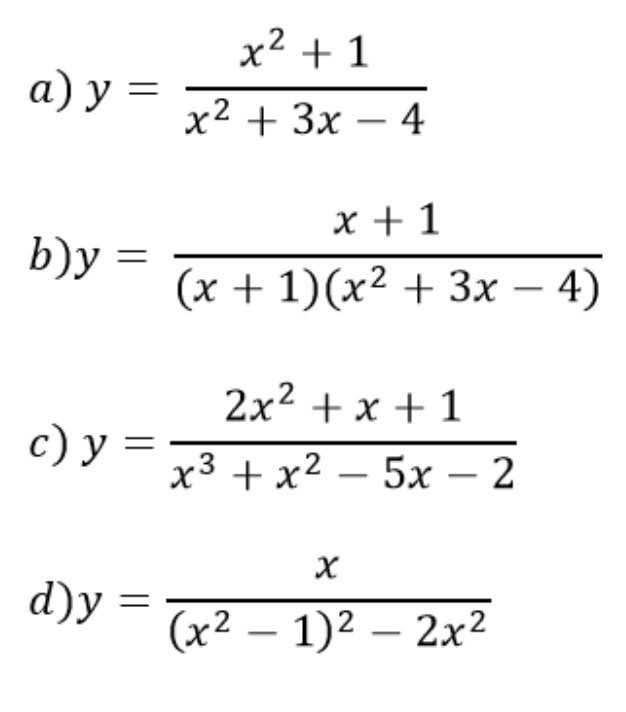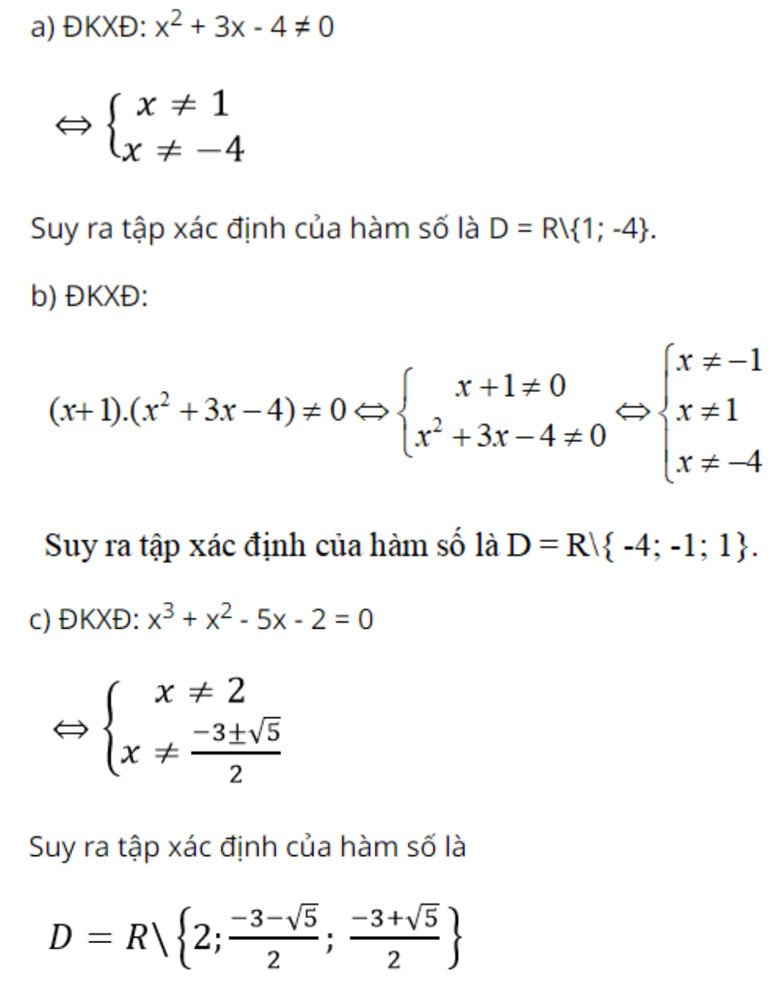Hàm số lượng giác là phần kiến thức mới nâng cao hơn sau khi chúng ta được học qua các bài học về giá trị lượng giác, công thức lượng giác ở lớp dưới. Với nội dung hôm nay, congthuctoanlyhoa.com sẽ điểm qua các hàm số lượng giác quan trọng và kèm theo các bài tập để các bạn luyện tập!
Hàm số sin
Ta xét hàm số y = sin x
– Tập xác định: D = R
– Tập giá trị: [-1;1]
– Hàm số tuần hoàn với chu kỳ 2π.
– Xét sự biến thiên:
– Đồ thị hàm số y = sin x là một đường hình sin
Do hàm số y = sin x là hàm số lẻ nên đồ thị nhận gốc tọa đồ làm tâm đối xứng
Hàm số cosin
Xét hàm số y = cos x
-Tập xác định: R
-Tập giá trị: [-1;1]
-Hàm số tuần hoàn với chu kỳ: 2π
-Xét sự biến thiên:
+ Hàm số đồng biến trên mỗi khoảng (-π +k2π; k2π), k ∈ Z
+ Hàm số nghịch biến trên mỗi khoảng (k2π; π + k2π). k ∈ Z
-Đồ thị hàm số y = cos x là một đường sin
Hàm số y = cos x là hàm số chẵn nên đồ thị nhận trục tung làm trục đối xứng
Hàm số tan
Hàm số y = tan x
-Tập xác định R { –π/2 + kπ; π/2 + kπ), k ∈ Z
-Đồ thị hàm số y = tan z
-Hàm số y = tan x là hàm số lẻ nên đồ thị nhận gốc tọa độ làm tâm đối xứng
-Đồ thị hàm số y = tan x có hình dạng như sau:
Hàm số cot
Hàm số y = cot x
-Tập xác định: R { kπ, (k ∈ Z)}
-Tập giá trị: R
-Hàm số y = cot x tuần hoàn với chu kỳ π.
-Hàm số nghịch biến trên mỗi khoảng (kπ; π + kπ), k ∈ Z.
-Đồ thị hàm số y = cot x nhận gốc tọa độ làm tâm đối xứng
Đồ thị hàm số y = cot x có hình dạng như sau:
Phương pháp giải bài tập hàm số lượng giác
Sau khi tìm hiểu qua các hàm số sin, cos, tan, cot của Đại số lớp 11, chúng ta sẽ học về các phương pháp giải bài tập để ứng dụng trong quá trình làm bài
Dạng 1: Tìm tập xác định của hàm số
Phương pháp làm bài: Chú ý đến tập xác định của hàm số lượng giác mà đề bài cho và tìm điều kiện của x để hàm số xác định.
Với dạng bài tập này, các bạn cần ghi nhớ các tập xác định của 4 hàm số ở trên.
Ví dụ: Tìm tập xác định của hàm số:
Như vậy, ta có thể giải bài toán này như sau:
Dạng 2: Xác định hàm chẵn, hàm lẻ
Phương pháp làm bài: Để xác định hàm số y = f(x) là hàm chẵn hay hàm lẻ, ta làm theo các bước sau
- Bước 1: Xác định tập xác định D của f(x)
- Bước 2: Với x bất kỳ x ∈ D , ta chứng minh -x ∈ D
- Bước 3: Tính f(-x)
– Nếu f(-x) = f(x), ∀x ∈ D => hàm số y = f(x) là hàm chẵn
– Nếu f(-x) = -f(x), ∀x ∈ D => hàm số y = f(x) là hàm lẻ.
– Nếu x ∈ D:
f(-x) ≠ f(x) => hàm số y = f(x) không là hàm chẵn
f(-x) ≠ -f(x) => hàm số y = f(x) không là hàm lẻ.
Ví dụ: Xét tính chẵn, lẻ của các hàm số y = tanx + 2sinx
Tập xác định D = {x|x ≠ π/2 + kπ, k∈Z}
Với x bất kỳ: x ∈ D và -x ∈ D:
Ta có: f(-x) = tan(-x) + 2 sin(-x) = -tanx – 2sinx = -(tanx + 2sinx) = -f(x), ∀x ∈ D
Kết luận, hàm số y = tanx + 2sinx là hàm số lẻ.
Dạng 3: Hàm số tuần hoàn và xác định chu kỳ tuần hoàn
Phương pháp giải: Để chứng minh y = f(x) (có TXĐ D) tuần hoàn, ta cần chứng minh có T ∈ R sao cho:
- x + T ∈ D; x – T ∈ D, ∀x ∈ D
- f(x + T) = f(x), ∀x ∈ D
Giả sử hàm số y = f(x) tuần hoàn, để tìm chu kỳ tuần hoàn ta cần tìm số dương T nhỏ nahast thỏa mãn hai tính chất vừa nêu trên
Ví dụ: Chứng minh hàm số y = f(x) = sin 2x tuần hoàn với chu kỳ π.
Ta có: D = R; x + π ∈ D, x – π ∈ D, ∀x ∈ D
f(x+π) = sin 2(x+π) = sin (2x + 2π) = sin 2x = f(x)
Kết luận. y = sin 2x là hàm số tuần hoàn với chu kỳ π
Dạng 4: Vẽ đồ thị hàm số và xác định các khoảng đồng biến và nghịch biến
Phương pháp làm bài:
- Bước 1: Vẽ đồ thị hàm số lượng giác đã cho theo dạng các hàm số lượng giác
- Bước 2: Dựa vào đồ thị hàm số vừa vẽ để xác định các khoảng đồng biến và nghịch biến của hàm số đó.
Ví dụ:
Dạng 5: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác
Phương pháp làm bài: Ta vận dụng tính chất -1 ≤ sin x ≤ 1, -1 ≤ cos x ≤ 1
Ví dụ: Tìm giá trị lớn nhất và nhỏ nhất của hàm số: y = 2sin(x – π/6) +3
Áp dụng tính chất trên ta có:
-1 ≤ sin(x – π/6) ≤ 1
=> 1 ≤ 2sin(x – π/6) +3 ≤ 5
Vậy GTNN là y = 1 khi sin(x – π/6) = -1 => x – π/6 = – π/2 + k2π
=> x = – π/3 + k2π, k ∈ Z
GTLN là y = 5 khi sin( x – π/6) =1 => x – π/6 = π/2 + k2π
=> x = 2π/3 + k2π, k ∈ Z.
Tổng kết
Với những nội dung quan trọng về Hàm số lượng giác hôm nay, congthuctoanlyhoa.com hy vọng đã giúp bạn đọc hiểu rõ hơn các phần lý thuyết cũng như bài tập thực hành liên quan. Chúc các bạn học tập thật tốt nhé!