Hàm số nói chung và hàm số bậc một, hàm số bậc hai là một trong những câu hỏi đầu tiên trong đề thi đại học, mức độ khó không cao nhưng đòi hỏi phải nắm vững lý thuyết và tính nhanh, chuẩn xác. Dưới đây là bài viết tổng hợp những phần lý thuyết quan trọng của nội dung này.
Hàm số bậc một Toán 10
Hàm số là gì?
Nếu một đại lượng y phụ thuộc vào một đại lượng thay đổi x sao cho một giá trị của x ta luôn xác định được một và chỉ một giá trị tương ứng của y. Khi đấy, y được gọi là hàm số của x, và x được gọi là biến số.
Ví dụ: y = 5x + 5
Khi x=2 thì y=15
Khi x=3 thì y=11
Mỗi giá trị x chỉ tìm được một và chỉ một giá trị y tương ứng.
Định nghĩa
Hàm số bậc một được hiểu là hàm số có dạng: y = ax + b. Trong đó, a và b là các số đã cho (a ≠ 0 và x là biến số).
Ví dụ: y = 2x + 5 là hàm số bậc nhất có biến số x và a= 2 ; b=5
Tính biến thiên
Hàm số bậc một y = ax + b (a≠0) có tập xác định D=R
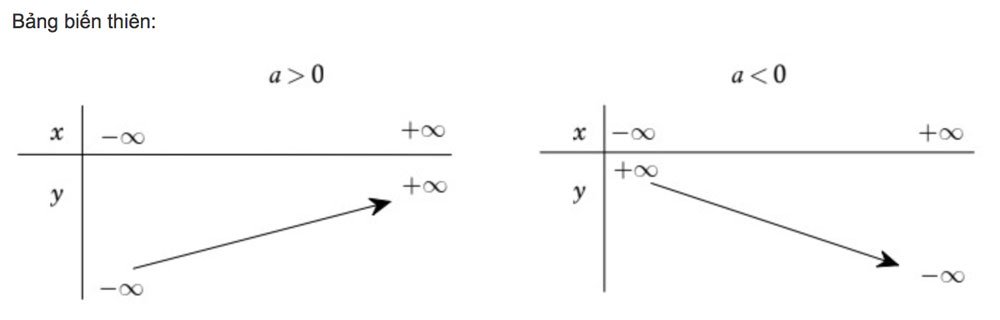
Hàm số này đồng biến trên R nếu a>0 và nghịch biến trên R nếu a<0.
Tính biến thiên của hàm số bậc nhất được thể hiện thông qua bảng biến thiên sau đây:
Cách vẽ đồ thị
Đồ thị hàm số bậc một y = ax + b (a ≠ 0) là một đường thẳng cắt trục tung tại điểm có tung độ bằng b, song song với đường thẳng y = ax (b ≠ 0) và trùng với đường thẳng y = ax (b = 0).
Đồ thị này cũng được gọi là đường thẳng y = ax + b và b được gọi là tung độ gốc của đường thẳng.
Lưu ý: Đồ thị y = ax + b cắt trục hoành tại điểm Q(-b/a; 0)
- Khi b = 0 thì đồ thị hàm số y = ax là đường thẳng đi qua gốc tọa độ O (0;0) và điểm A (1;a) đã biết.
- Trong trường hợp y = ax + b (a ≠ 0, b ≠ 0) thì đồ thị hàm số y = ax + b là một đường thẳng. Vì vậy, các em chỉ cần xác định được hai điểm phân biệt nào đó của đồ thị rồi vẽ đường thẳng đi qua hai điểm đó. Cụ thể:
- Xác định giao điểm của đồ thị hàm số với hai trục của tọa độ. Cho x = 0, tính được y = b và ta có điểm A (0;b). Cho y = 0, tính được x = – b/a và ta có điểm B (- b/a;0).
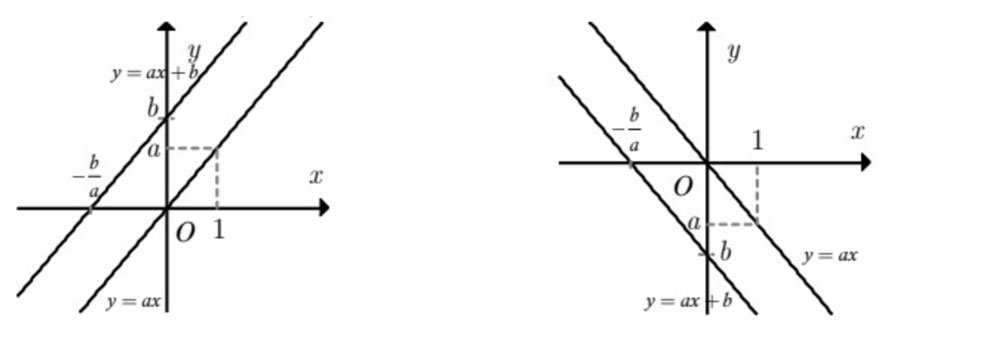
- Vẽ đường thẳng đi qua hai điểm A và B, ta được đồ thị hàm số y = ax + b có dạng như sau:
Chú ý:
Khi vẽ đồ thị hàm số y=ax+b; a≠0, ta nên chọn hai điểm có tọa độ chẵn
Thông thường ta chọn hai điểm A(0;b) và B(-b/a;0) theo thứ tự giao điểm của đồ thị với trục Oy và Ox, nếu hai điểm đó không nằm quá xa gốc tọa độ hoặc tọa độ của chúng không quá phức tạp trong tính toán.
Hàm số bậc hai Toán 10
Định nghĩa
Theo chuẩn kiến thức của bộ giáo dục, hàm số bậc hai được định nghĩa như sau:
- Hàm số bậc hai là hàm số có công thức y=ax2+bx+c(a≠0) và có miền xác định D=R
- Trường hợp có 2 biến x và y, hàm số có dạng f(x,y) = ax2+by2+cxy+dx+ey+fKhi đó nó cùng với hàm chuẩn mẫu tạo trên hệ trục tọa độ những hình cônic (parabol, elip, tròn hoặc hyperbol)
Hàm số bậc hai đồng biến khi nào?
Hàm số bậc hai đồng biến nếu:
- Hàm số f(x) được gọi là đồng biến trên K (K là một khoảng, một đoạn hay nửa đoạn), nếu với mọi cặp x1, x2 ∈ K mà x1 < x2 thì f(x1) < f(x2).
- Cho hàm số y=f(x) có đạo hàm f′(x) trên K. Nếu f′(x) ≥ 0, ∀x ∈ K, f′(x) = 0 chỉ tại một số hữu hạn điểm thì f(x) đồng biến
Hàm số bậc hai nghịch biến khi nào?
Hàm số bậc hai nghịch biến khi:
- Hàm số f(x) được gọi là nghịch biến trên K, nếu với mọi cặp x1, x2 ∈ K mà x1 < x2 thì f(x1) > f(x2).
- Cho hàm số y = f(x) có đạo hàm f′(x) trên K. Nếu f′(x) ≤ 0, ∀x ∈ K, f′(x) = 0 chỉ tại một số hữu hạn điểm thì f(x) nghịch biến.
Cực trị
- Giả sử hàm số y = f(x) đạt cực trị tại x0. Khi đó, nếu y = f(x) có đạo hàm tại x0 thì f′(x0) = 0.
- Giả sử hàm số y = f(x0) liên tục trên khoảng (a;b) chứa x0 và có đạo hàm trên (a;x0),(x0;b).
Khi đó:
- Nếu f′(x) < 0, ∀x∈ (a;x0) và f′(x) > 0, ∀x ∈ (x0;b) thì hàm số y = f(x) đạt cực tiểu tại x0.
- Nếu f′(x) > 0, ∀x∈ (a;x0) và f′(x) < 0, ∀x ∈ (x0;b) thì hàm số y = f(x) đạt cực đại tại x0.
Giả sử hàm số y=f(x) có đạo hàm cấp một trên (a;b) và có đạo hàm cấp hai khác 0 tại x0. Khi đó:
- Nếu f′(x0) = 0; f”(x0) < 0 thì hàm số đạt cực đại tại x0
- Nếu f′(x0) = 0; f”(x0) > 0 thì hàm số đạt cực tiểu tại x0
Lưu ý: Nếu f”(x0) = 0 thì hàm số có thể đạt cực trị hoặc không đạt cực trị tại x0.
Cách lập bảng biến thiên
Để lập bảng biến thiên hàm số bậc hai, ta làm lần lượt theo các bước sau đây:
- Bước 1: Tìm tập xác định.
- Bước 2: Tính y′. Tìm các điểm tại đó y′ bằng 0 hoặc không xác định.
- Bước 3: Lập bảng biến thiên. Từ bảng biến thiên rút ra kết luận.
Cách vẽ đồ thị
Để vẽ đường parabol y = ax2 + bx + c (a≠0), ta thực hiện các bước sau:
- Xác định tọa độ đỉnh là điểm I(−b2/a;−Δ/4a)
- Vẽ trục đối xứng d là đường thẳng x=−b/2a
- Xác định giao điểm của parabol với các trục tọa độ (nếu có). Xác định thêm một số điểm thuộc đồ thị. Chẳng hạn, điểm đối xứng với giao điểm của đồ thị với trục tung qua trục đối xứng của parabol.
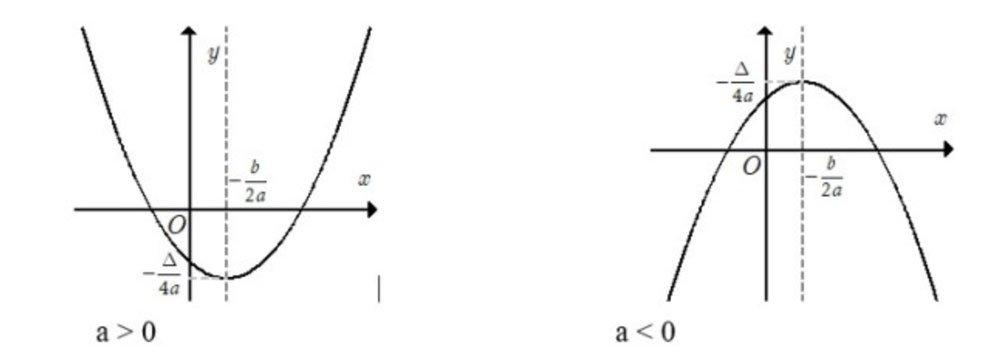
- Vẽ parabol dựa vào kết quả trên
Chú ý:
- Bề lõm của đường cong parabol hướng lên trên nếu a>0 và hướng xuống khi a<0
- Hoành độ giao điểm với trục hoành (nếu có) là nghiệm của phương trình: ax2 + bx + c = 0
- Các dạng toán hàm số bậc nhất và hàm số bậc hai
Các dạng toán hàm số bậc một và hàm số bậc hai
Dưới đây là những dạng bài tập của Đại số 10 liên quan đến hàm số bậc một và hàm số bậc hai:
Bài toán về hàm số bậc một:
Dạng 1: Xác định hàm số y = ax + b và sự tương giao của đồ thị hàm số
Dạng 2: Xét sự biến thiên và vẽ đồ thị hàm số bậc một
Dạng 3: Đồ thị hàm số chứa dấu giá trị tuyệt đối
Dạng 4: Ứng dụng của hàm số bậc một chứng minh bất đẳng thức và tìm giá trị lớn nhất, giá trị nhỏ nhất
Bài toán về hàm số bậc hai:
Dạng 1: Xác định hàm số bậc hai
Dạng 2: Xét sự biến thiên và vẽ đồ thị hàm số bậc hai
Dạng 3: Đồ thị hàm số chứa dấu giá trị tuyệt đối và cho bởi nhiều công thức
Tổng kết
Hi vọng thông qua bài viết này, congthuctoanlyhoa.com đã có thể giúp bạn hiểu rõ hơn những kiến thức về hàm số, hàm số bậc một và hàm số bậc hai. Tiếp tục theo dõi kênh để có thể bổ sung thêm những kiến thức về toán, lý, hóa lớp 9, 10, 11 và 12.