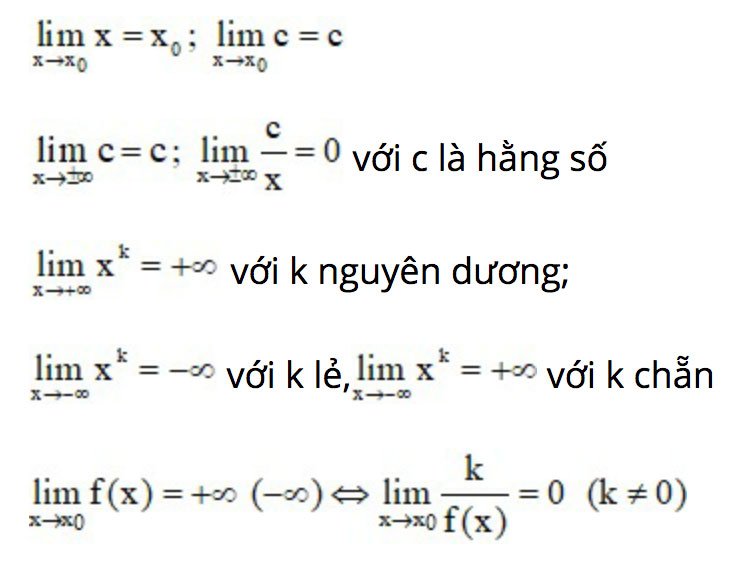Giới Hạn là chương mở đầu cho môn học Đại số lớp 11 và được áp dụng xuyên suốt nhiều bài tập cơ bản lẫn nâng cao. Hôm nay, congthuctoanlyhoa.com sẽ cùng các bạn tổng hợp lý thuyết và bài tập về Giới hạn nhé!
Khái niệm Giới hạn
Trong Toán học, khái niệm “giới hạn” được sử dụng để chỉ giá trị mà một dãy số hoặc hàm số tiến gần đến khi biến số tương ứng tiến gần đến một giá trị nào đó.
Ký hiệu của Giới hạn được viết là lim . Khi muốn chỉ a là giới hạn của dãy số (an) ta viết lim(an) = a hoặc an → a.
Vậy giới hạn của dãy số và hàm số như thế nào, ta cùng tìm hiểu phần tiếp theo.
Giới hạn của dãy số
Giới hạn hữu hạn
Dãy số (un)được gọi là có giới hạn bằng 0 khi n tiến ra dương vô cực nếu với mỗi số dương nhỏ tùy ý cho trước, mọi số hạng của dãy số, kể từ một số hạng nào đó trở đi, đều có giá trị tuyệt đôi nhỏ hơn số dương đó.
Ta có kí hiệu: hay un → 0 khi n → +∞.
Dãy số (un) có giới hạn là số thực gọi là dãy số có giới hạn hữu hạn
Lưu ý, một số giới hạn đặc biệt
Giới hạn vô cực
– Ta nói dãy số (un) có giới hạn là +∞ khi n → +∞, nếu un có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Kí hiệu: lim un = +∞ hay un → +∞ khi n → +∞.
– Dãy số (un) có giới hạn là –∞ khi n → +∞, nếu lim (–un) = +∞.
Kí hiệu: lim un = –∞ hay un → –∞ khi n → +∞.
Nhận xét: un = +∞ ⇔ lim(–un) = –∞
Lưu ý một số kết quả đặc biệt như sau:
- lim nk = +∞ với mọi k > 0
- lim qn= +∞ với mọi 1 > 0
Một vài giới hạn đặc biệt
Ta thừa nhận các kết quả sau:
a) lim nk = +∞ với k nguyên dương;
b) lim qn = +∞ nếu q > 1.
Một số định lý về giới hạn
Với các bài toán về giới hạn, ta có thể áp dụng các định lý sau theo sách giáo khoa Đại số lớp 11
Định lý 1:
Nếu dãy số (un) thỏa | un | < vn kể từ số hạng nào đó trở đi và lim vn = 0 thì
lim un = 0
Định lý 2:
Cho lim un = a, lim vn = b. ta có
- lim (un + vn) = a + b
- lim (un – vn) = a – b
- lim(un.vn) = a.b
- lim (un/vn) = a/b (b khác 0)
- Nếu un ≥ 0∀ thì lim √un = √a
Tổng của cấp số nhân lùi vô hạn
Tổng của CSN lùi vô hạn
Cấp số nhân vô hạn u1, u2, u3,..un,..có công bội q, với |q| < 1 gọi là cấp số nhân lùi vô hạn.
Tổng S của cấp số nhân đó là:
Giới hạn của hàm số
a) Giới hạn của hàm số tại một điểm:
* Giới hạn hữu hạn:
Cho khoảng K chứa điểm x0 . Ta nói rằng hàm số f(x) xác định trên K (có thể trừ điểm x0) có giới hạn là L khi x dần tới x0 nếu với dãy số (xn) bất kì, xn ∈ K \ {x0} và xn → x0, ta có: f(xn) → L.
Kí hiệu: hay f(x) → L khi x → x0.
Nhận xét: Nếu f(x) là hàm số sơ cấp xác định tại x0 thì
* Giới hạn ra vô cực:
Hàm số y = f(x) có giới hạn dần tới dương vô cực khi x dần tới x0 nếu với mọi dãy số (xn): xn → x0 thì f(xn) → +∞.
Kí hiệu:
Hàm số y = f(x) có giới hạn dần tới âm vô cực khi x dần tới x0 nếu với mọi dãy số (xn): xn → x0 thì f(xn) → −∞.
Kí hiệu:
b) Giới hạn của hàm số tại vô cực
* Giới hạn ra hữu hạn:
– Ta nói hàm số y = f(x) xác định trên (a;+∞) có giới hạn là L khi x → +∞ nếu với mọi dãy số (xn): xn > a và xn → +∞ thì f(xn) → L.
Kí hiệu:
– Ta nói hàm số y = f(x) xác định trên (−∞;b) có giới hạn là L khi x → −∞ nếu với mọi dãy số (xn): xn < b và xn → −∞ thì f(xn) → L.
Kí hiệu:
* Giới hạn ra vô cực:
– Ta nói hàm số y = f(x) xác định trên (a;+∞) có giới hạn dần tới dương vô cùng (hoặc âm vô cùng) khi x → +∞ nếu với mọi dãy số (xn): xn > a và xn → +∞ thì f(xn) → +∞ (hoặc f(xn) → −∞).
Kí hiệu:
– Ta nói hàm số y = f(x) xác định trên (−∞; b) có giới hạn là dần tới dương vô cùng (hoặc âm vô cùng) khi x → −∞ nếu với mọi dãy số (xn): xn < b và xn → −∞ thì f(xn) → +∞ (hoặc f(xn) → −∞).
Kí hiệu:
Giới hạn một bên
- Cho hàm số y = f(x) xác định trên (x0;b). Số L gọi là giới hạn bên phải của hàm số y = f(x) khi x dần tới x0 nếu với mọi dãy (xn): x0 < xn < b mà xn → x0
thì ta có :f(xn) → L.
- Cho hàm số y = f(x) xác định trên (a;x0). Số L gọi là giới hạn bên trái của hàm số y = f(x) khi x dần tới x0 nếu với mọi dãy (xn) : a < xn < x0 mà xn → x0 thì ta có: f(xn) → L
Giới hạn vô cực
- Ta nói hàm số y = f(x) có giới hạn dần tới dương vô cực khi x dần tới x0 nếu với mọi dãy số (xn) : xn → x0 thì f(xn) → +∞
- Tương tự ta cũng có định nghĩa giới hạn dần về âm vô cực
- Ta cũng có định nghĩa như trên khi ta thay x bởi –∞ hoặc +∞
Các định lý về giới hạn
Ta có thêm một số giới hạn đặc biệt như sau:
Tổng kết
Như vậy, Công thức Toán Lý Hóa đã vừa điểm qua các kiến thức quan trọng trong bài Giới hạn của chương trình Toán học lớp 11. Hy vọng bài viết đã giúp cho các bạn hiểu rõ và nắm được các lưu ý đặc biệt để áp dụng bào tập nhuần nhuyễn hơn.