Trong đời sống thường nhật, ta đã thấy nhiều vật dụng có hình cầu, như trái bóng đá, trái cam, golf…Và bài viết này congthuctoanlyhoa sẽ giới thiệu đến các bạn học sinh về hình cầu cùng công thức tính diện tích và thể tích của nó một cách chi tiết nhất. Ngoài ra, đây cũng là bài cuối cùng của chương trình THCS phân môn hình học, cũng là kiến thức nền tảng để các bạn chinh phục được chương trình THPT một cách tự tin nhất.
Định nghĩa hình cầu cụ thể
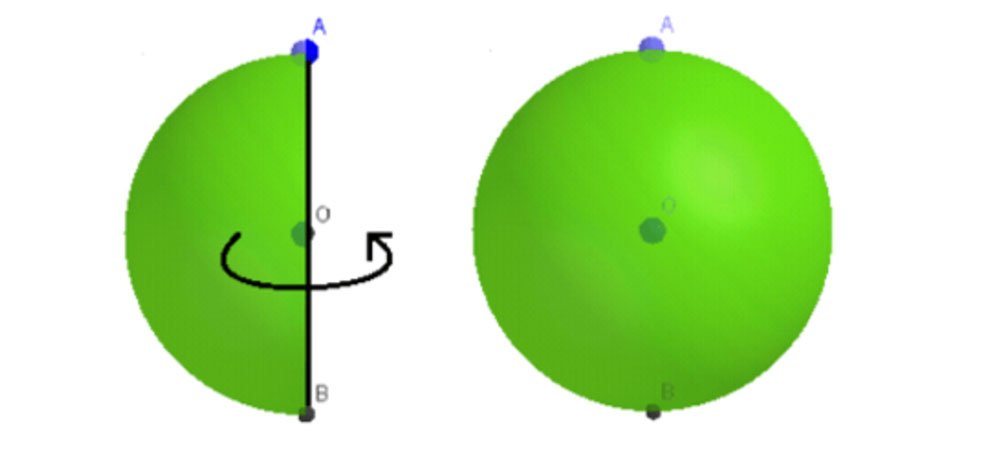
Khi quay nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định thì được một hình cầu
- Nửa đường tròn trong phép quay nói trên tạo thành một mặt cầu.
- Điểm O được gọi tâm, R là bán kính của hình cầu hay mặt cầu đó.
Cắt hình cầu bởi mặt phẳng
Chúng ta có các tính chất sau:
- Bất kỳ mặt phẳng nào cắt qua mặt cầu, ta đều nhận được mặt cắt là hình tròn
- Bất kỳ mặt phẳng nào cắt mặt cầu, ta được một đường tròn, trong đó:
- Đường tròn đó có bán kính = R nếu mặt phẳng đi qua tâm (đường tròn lớn)
- Đường tròn đó có bán kính < R nếu mặt phẳng không đi qua tâm
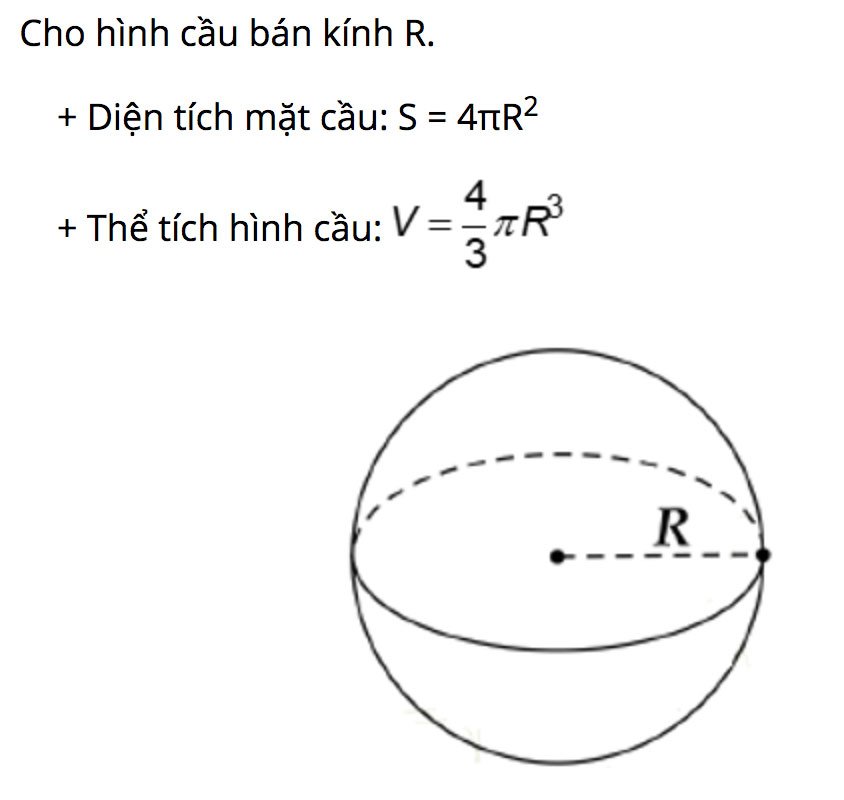
Công thức tính diện tích mặt cầu và thể tích hình cầu
Cho hình cầu có bán kính R, đường kính d
Các dạng toán thường gặp về hình cầu
Hình cầu là một trong những bài quan trọng của chương trình Hình Học Lớp 9, các bạn học sinh cố gắng ghi chép và luyện tập cẩn thận.
Dạng 1: Tính diện tích mặt cầu, thể tích hình cầu và bán kính hình cầu.
Phương pháp:
Ta sử dụng các công thức tính diện tích mặt cầu S = 4πR2 và thể tích hình cầu V = (4/3)πR3.
Dạng 2: Bài toán tổng hợp
Phương pháp:
Vận dụng các công thức trên và các kiến thức đã học để tính các đại lượng chưa biết rồi từ đó tính diện tích mặt cầu, thể tích hình cầu.
Bài tập minh họa hình cầu
Bài tập cơ bản
Bài 1:Tính diện tích của mặt cầu có bán kính R = 3cm.
Theo công thức, ta có diện tích mặt cầu là: S = 4R2π= 4.32.π = 32π(cm2)
Bài 2:Khi bán kính của một mặt cầu tăng lên 3/2 lần thì diện tích và thể tích sẽ thay đổi như thế nào?
Dựa theo công thức, khi R tăng 3/2 thì diện tích tăng lên R2 lần tức là 9/4 lần.
Tương tự đối với thể tích V = (4/3)πR3
Khi R tăng lên 3/2 thì thể tích tăng lên R3, tức là 27/8 lần.
Bài tập nâng cao
Giả sử trái cam có hình tương tự như mặt cầu, bạn Lan cắt trái cam làm đôi và tiến hành đo đường kính của nửa trái cam vừa cắt, bạn đo được bán kính tính cả vỏ cam là 2,5cm, biết vỏ cam dày 3mm. Hãy tính thể tích thực của quả cam đó.
Lời giải:
Xem như phần cam đã mà Lan đã ăn cũng là một dạng mặt cầu, vậy bán kính của mặt cầu ấy chính là bán kính của quả cam đó trừ đi vỏ.
Tổng kết
Bài viết đã tổng kết và hệ thống lại tất cả lý thuyết về hình cầu cũng như công thức tính diện tích và thể tích của nó. Qua đây, Công Thức Toán Lý Hóa mong rằng các bạn học sinh lớp 9 sẽ nắm được căn bản của bài học này cũng như các bài khác trong phân hình học để có thể tự tin chinh phục chương trình học THPT sắp tới. Chúc các bạn đạt thành tích cao trong học tập.