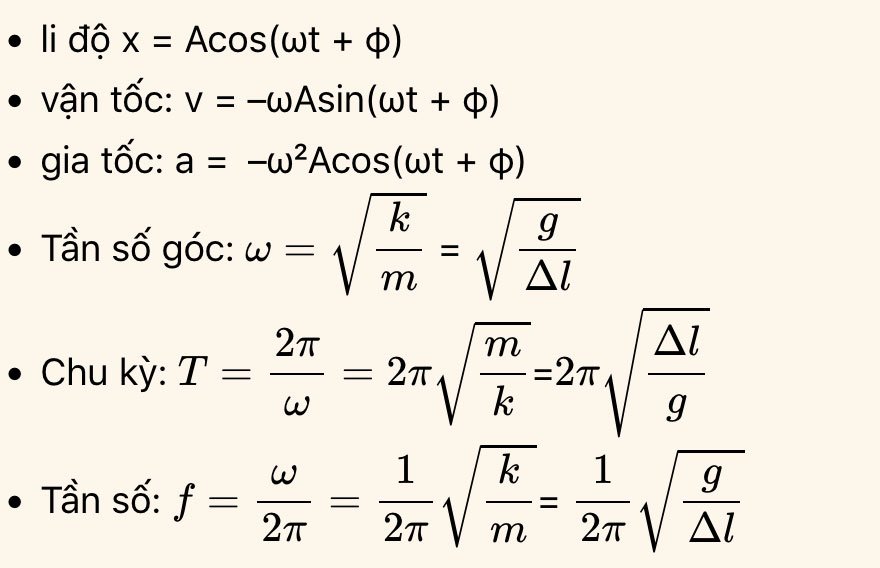[Vật lý 12] Lý thuyết và bài tập dao động điều hòa

Bài viết tổng hợp toàn bộ lý thuyết và các dạng bài tập của phần dao động điều hòa – kiến thức vật lý lớp 12.

Lý thuyết dao động điều hòa

Khái niệm

• Dao động cơ: là chuyển động qua lại quanh một vị trí cân bằng ( vị trí hợp lực tác dụng lên vật bằng không). VD: chuyển động đung đưa của chiếc lá,…
• Dao động tuần hoàn: là dao động cơ mà sau những khoảng thời gian bằng nhau vật trở lại vị trí cũ theo hướng cũ. Khi vật trở lại vị trí cũ theo hướng cũ thì vật thực hiện được một dao động toàn phần. Thời gian vật thực hiện một dao động toàn phần là một chu kỳ T. Số dao động toàn phần vật thực hiện được trong 1s là tần số f.

+) Quá trình từ B → C → B: vật trở về cùng một vị trí nhưng không cùng chiều nên không phải là một dao động toàn phần.

+) Quá trình B → C → B → A → B: là một dao động toàn phần.

• Dao động điều hòa: là dao động trong đó li đô (vị trí) của vật là một hàm côsin (hay sin) của thời gian.

Các đại lượng đặc trưng của dao động điều hòa

Chu kì

Chu kì là khoảng thời gian để vật thực hiện được một dao động toàn phần.

Đơn vị của chu kì là s (giây).

Tần số dao động

Tần số f là số dao động toàn phần thực hiện được trong một giây.

Đơn vị của tần số là Hz (héc)

Tần số góc

Tần số góc ω là đại lượng liên hệ với chu kì T hay với tần số f qua hệ thức dưới đây.

• Đơn vị của tần số góc là rad/s.
• Một chu kì dao động vật đi được quãng đường là S = 4A.
• Chiều dài quỹ đạo chuyển động của vật là L = 2A.

Vận tốc dao động điều hòa

v = x’ = –ωA.sin(ωt + φ) = ωAcos(ωt + φ + π/2)

→ Độ lớn v_max = ωA tại vị trí cân bằng x = 0; v = 0 tại vị trí biên x = ±A

– Gia tốc a = v’ = x”= -ω²A = -ω² A cos⁡(ωt + φ) = ω² A cos⁡(ωt+φ + π)

→ Độ lớn a_max = ω² A tại vị trí biên x = ±A; a = 0 tại vị trí cân bằng x = 0

Gia tốc dao động điều hòa

a = v’ = x” = –ω²A.cos(ωt + φ) = ω²A.sin(ωt + φ + π/2) = –ω²x

a${}_{max}$= ω²A tại biên âm (x = –A)

Giá trị cực tiểu a${}_{CT}$= –ω²A tại biên dương (x = A)

độ lớn cực tiểu: a${}_{min}$= 0 tại vị trí cân bằng (x = 0)

Trong đó:

• Li độ x: khoảng cách từ vị trí của vật đến vị trí cân bằng.
• Biên độ A = x${}_{max}$
• ω: tần số góc (rad/s)
• ωt + φ: pha dao động
• φ: pha ban đầu của dao động
• vận tốc sớm pha hơn li độ góc π/2
• v > 0 vật chuyển động theo chiều dương
• v < 0 vật chuyển động theo chiều âm
• từ VTCB → biên: vật chuyển động chậm dần
• từ biên → VTCB: vật chuyển động nhanh dần
• gia tốc a sớm pha hơn vận tốc góc π/2
• gia tốc a –ω²x => a ngược pha với li độ x
• $\overrightarrow{a}$
• có chiều luôn hướng về vị trí cân bằng
• $\overrightarrow{a}$↑↑$\overrightarrow{v}$khi vật chuyển động từ biên về VTCB

• $\overrightarrow{a}$↑↓$\overrightarrow{v}$ khi vật chuyển động từ VTCB ra biên

Mối quan hệ giữa li độ (x), vận tốc (v) và gia tốc (a)

Phương trình dao động điều hòa

Bài tập dao động điều hòa

Trong chương trình Vật lý 12, phần kiến thức dao động điều hòa thường có những dạng bài tập sau:

Dạng 1: Xác định các đại lượng đặc trưng trong bài tập dao động điều hòa

Đây là dạng toán xác định đại lượng như biên độ A, vận tốc góc ω, chu kỳ, tần số, pha ban đầu từ một số dữ kiện cho trước … bằng cách đồng nhất với phương trình dao động điều hòa chuẩn.

– Dao động điều hòa được xem là một dao động mà li độ của vật được mô tả bằng hàm cosin hay sin theo biến thời gian. Một cách khác, một dao động điều hòa có phương trình là nghiệm của phương trình vi phân: x’’ + ω²x = 0 có dạng như sau:

x = Acos(ωt + φ)

Trong đó:

+ x: Li độ, li độ là khoảng cách từ vật đến vị trí cân bằng ( Đơn vị độ dài)

+ A: Biên độ (li độ cực đại) ( Đơn vị độ dài)

+ ω: Vận tốc góc (rad/s)

+ ωt + φ: Pha dao động (rad/s) tại thời điểm t, cho biết trạng thái dao động của vật ( gồm vị trí và chiều )

+ φ : Pha ban đầu (rad) tại thời điểm t = 0s, phụ thuộc vào cách chọn gốc thời gian, gốc tọa độ.

Chú ý: φ, A là những đại lượng hằng, lớn hơn 0.

– Phương trình vận tốc v (m/s)

v = x’ = ωAcos(ωt + φ + π/2)

Suy ra: v_max = ωA Tại vị trí cân bằng x = 0, vmin = 0 đạt được tại 2 biên.

Dạng 2: Tìm quãng đường vật đi được trong các dao động điều hòa

Lưu ý: 

+ Trong thời gian t = 1T vật đi được quãng đường S = 4A

+ Trong thời gian nửa chu kỳ T vật đi được quãng đường S = 2A

– Bước 1: Xác định vị trí hoặc thời điểm t₁, t₂ cho trước trên đường tròn. Tìm Δt, Δt = t₂ – t₁.

– Bước 2: Tách Δt = n.T + t* ⇔ Δφ = n.vong + φ*

– Bước 3: Tìm quãng đường. S = n.4.A + S*.

Căn cứ vào vị trí và chiều chuyển động của vật tại t₁ và t₂ để tìm ra S₃

Dạng 3: Tính toán tốc độ trung bình, vận tốc trung bình trong bài tập dao động điều hòa

a) Tổng quát:

v = S/t

Trong đó:

– S: quãng đường đi được trong khoảng thời gian t

– t: là thời gian vật đi được quãng đường S

b) Bài toán tính tốc độ trung bình cực đại của vật trong khoảng thời gian t:

v_max = S_max/t

c) Bài toán tính tốc độ trung bình nhỏ nhất vật trong khoảng thời gian t.

v_min = S_min/t

d) Vận tốc trung bình

v_tb = Δx/t

Trong đó:

+ Δx: là độ biến thiên độ dời của vật

+ t: thời gian để vật thực hiện được độ dời Δx

Tổng kết

Thông qua bài viết trên, congthuctoanlyhoa.com hi vọng bạn đã nắm vững được kiến thức lý thuyết cũng như bài tập của phần dao động điều hòa – phần kiến thức đặc biệt quan trọng, thường xuyên xuất hiện trong các kì thi.