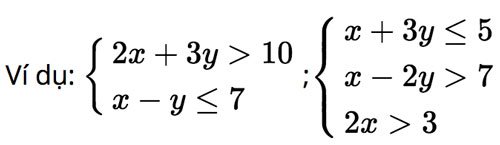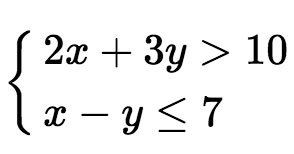[Toán 10] Bất phương trình và hệ bất phương trình bậc nhất hai ẩn

Bài viết truyền tải các kiến thức về bất phương trình (BPT) và hệ bất phương trình bậc nhất hai ẩn như: tóm tắt lý thuyết, biểu diễn tập nghiệm, giải bài tập và các đề thi để ôn tập lại kiến thức.

Bạn đang đọc bài viết: [Toán 10] Bất phương trình và hệ bất phương trình bậc nhất hai ẩn

Bất phương trình bậc nhất hai ẩn

Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là $ax+by\le c\left(1\right)$

($ax+by>c,ax+by\ge c,ax+by<c$)

trong đó $a,b,c$ là các số đã cho với $a,\; b$ không đồng thời bằng 0 và x, y là các ẩn số.

Cặp số $(x_0;y_0)$ sao cho $a{x}_0+b{y}_0\le c$ là một bất đẳng thức đúng được gọi là một nghiệm của BPT $ax+by\le c$

Xem thêm [TOÁN 9] Phương trình bậc 2 một ẩn, cách giải và tính nhẩm siêu tốc [MỚI NHẤT]

Miền nghiệm của bất phương trình bậc nhất hai ẩn

Định nghĩa

Trong mặt phẳng tọa độ, thì mỗi nghiệm của bất phương trình bậc nhất hai ẩn ax + by $\le c$ biểu diễn bởi mộtđiểm và tập nghiệm của nó được biểu diễn bởi một tập hợp điểm, ta gọi tập hợp điểm ấy là miền nghiệm của bất phương trình.

Định lý

Cho mặt phẳng tọa độ, đường thẳng (d): ax + by + c =0 chia mặt phẳng thành hai nửa mặt phẳng sao cho một trong hai nửa mặt phẳng ấy (không kể bờ (d)) gồm các điểm tọa độ thỏa mãn BPT ax + by + c > 0, nửa mặt phẳng còn lại (không kể bờ (d)) gồm các điểm có tọa độ thỏa mãn BPT ax + by + c < 0. Từ đó ta suy ra:

Nửa mặt phẳng (không kể bờ (d) chứa M(x0;y0) là miền nghiệm của BPT ax+by+c>0 (hay ax+by+c<0) nếu M(x0;y0) là nghiệm của BPT đó.

Biểu diễn miền nghiệm bất phương trình bậc nhất hai ẩn

Quy tắc biểu diễn hình học tập nghiệm của $ax+by\le c\left(1\right)$ như sau:

+ Bước 1: Trên mặt phẳng tọa độ Oxy vẽ đường thẳng $ax+by=c\left(d\right)$

+ Bước 2: Lấy một điểm $M_0(x_0;y_0)$ không thuộc (d) (ta thường lấy gốc tọa độ)

+ Bước 3: Tính $a{x}_0+b{y}_0$ và so sánh với c.

+ Bước 4: Kết luận

Nếu $a{x}_0+b{y}_0<c$ thì nửa mặt phẳng bờ (d) chứa M0 là miền nghiệm của $ax+by\le c$.

Nếu $a{x}_0+b{y}_0>c$ thì nửa mặt phẳng bờ (d) không chứa $M_0$ là miền nghiệm của $ax+by\le \mathrm{c.}$

Chú ý:.

Đối với các BPT dạng ax+by+c≤0 hoặc ax+by+c≥0 thì miền nghiệm là nửa mặt phẳng kể cả bờ.

BPT bậc nhất hai ẩn luôn có vô số nghiệm.

Ví dụ về biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn:

Xác định miền nghiệm của bất phương trình: 2x-y ≥ 0

Hệ bất phương trình bậc nhất hai ẩn

Định nghĩa: Hệ bất phương trình bậc nhất hai ẩn gồm một số BPT bậc nhất hai ẩn x, y mà ta phải tìm các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ BPT đã cho.

Cũng như BPT bậc nhất hai ẩn, ta có thể biểu diễn hình học tập nghiệm của hệ BPT bậc nhất hai ẩn.

Cách xác định miền nghiệm:

Bước 1: Xác định miền nghiệm của từng bất phương trình.

Bước 2: Phần còn lại không gạch chéo trong mặt phẳng tọa độ chính là miền nghiệm của hệ BPT đã cho.

Hướng dẫn giải các dạng bài tập

Xác định miền nghiệm của bất phương trình và hệ bất phương trình bậc nhất hai ẩn

Xác định miền nghiệm của bất phương trình bậc nhất hai ẩn

Trong mặt phẳng tọa độ, vẽ đường thẳng Δ: x + 4y + 2 = 0.
Xét điểm O(0;0), ta thấy (0;0) không phải là nghiệm của BPT đã cho do đó miền nghiệm cần tìm là nửa mặt phẳng bờ Δ (không kể đường thẳng Δ) và không chứa điểm O(0;0) (miền không được tô màu trên hình vẽ).

Vẽ các đường thẳng (d): x + y − 2 = 0, (d′): x − 3y + 3 = 0 trên mặt phẳng tọa độ Oxy.
Xét điểm O(0;0), thấy (0;0) không phải là nghiệm của BPT x+y−2≥0 và x−3y+3≤0.
Do đó miền nghiệm cần tìm là phần mặt phẳng không được tô màu trên hình vẽ kể cả hai đường thẳng (d) và (d′).

Ứng dụng để giải bài toán về kinh tế

Trong Đại số 10 thì bất phương trình và hệ bất phương trình bậc nhất hai ẩn còn dùng để giải các bài toán kinh tế trong thực tế.

Ví dụ:

Một xưởng sản xuất hai loại sản phẩm, mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, đem lại mức lời 40000 đồng. Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, đem lại mức lời 30000 đồng. Xưởng có 200 kg nguyên liệu và 120 giờ làm việc. Nên sản xuất mỗi loại sản phẩm bao nhiêu để có mức lời cao nhất?

Phân tích bài toán: Gọi x (x$\ge 0)\; là\; số\; kg\; loại\; I\; cần\; sản\; xuất,\; y\; (y\ge 0)\; là\; số\; kg\; loại\; II\; cần\; sản\; xuất.$

Suy ra số nguyên liệu cần dùng là: 2x + 4y, thời gian là 30x + 15y có mức lời là 40000x + 30000y

Theo giả thiết bài toán xưởng có 200 kg nguyên liệu và 120 giờ làm việc.

Suy ra: 2x + 4y $\le \; 200\; hay\; x\; +\; y\; –\; 100\; \le \; 0,3x\; +\; 15y\; \le \; 1200\; hay\; 2x\; +\; 8y\; \le \; 0$

Bài toán trở thành: Tìm x, y thỏa mãn hệ:

sao cho L(x;y) = 40000x + 30000y đạt giá trị lớn nhất.

Trong mặt phẳng tọa độ vẽ các đường thẳng (d) : x + 2y – 100 + 0, (d”): 2x + y – 80 + 0

Khi đó miền nghiệm của hệ bất phương trình trên là phần mặt phẳng (tứ giác) không tô màu lên hình vẽ

Giá trị lớn nhất của L(x;y) = 40000x + 30000y đạt tại một trong các điểm (0;0) , (40;0) , (0;50) , (20;40). Ta có: L(0;0) = 0 , L(40;0) = 1600000, L(0;50) = 1500000, L(20;40) = 2000000

Suy ra giá trị lớn nhất của L(x;y) là 2000000 khi (x;y) = (20;40)

Vậy cần sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II để có mức lời lớn nhất.

Tổng kết 

Trên đây là toàn bộ kiến thức về bất phương trình và hệ bất phương tình bật nhất hai ẩn của chương tình toán học cấp phổ thông. Hi vọng thông qua bài viết này, congthutoanlyhoa.com đã có thể giúp các bạn nắm vững được kiến thức về lý thuyết và giải được các bài tập thuộc phần này.