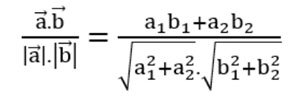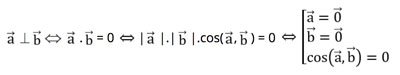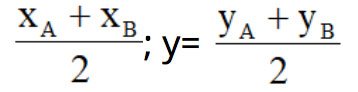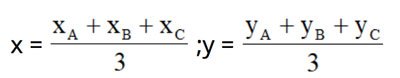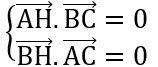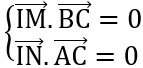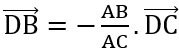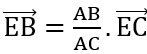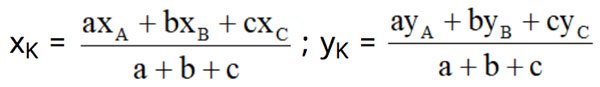Các dạng bài Công thức tích vô hướng của hai vectơ

Dạng 1: Tính tích vô hướng của hai vectơ, góc giữa hai vectơ.

Phương pháp giải: 

– Tính tích vô hướng: Phân tích vectơ và đưa hai vectơ về chung gốc để tìm góc giữa hai vectơ hoặc đưa hai vectơ về các vectơ vuông góc. Sau đó, áp dụng công thức định nghĩa, tính chất và hằng đẳng thức để tính tích vô hướng của hai vectơ. Đối với hai vectơ biết tọa độ thì tính theo công thức  = a₁b₁ + a₂b₂

– Tính góc giữa hai vectơ: Phân tích vectơ và đưa hai vectơ về chung gốc để tìm góc giữa hai vectơ hoặc dùng công thức:

Dạng 2: Tính độ dài đoạn thẳng, độ dài vectơ. 

Phương pháp giải:

Phân tích vectơ để biến phép tính độ dài đoạn thẳng thành phép tính tích vô hướng, áp dụng công thức  . Nếu đề bài có liên quan đến tọa độ thì áp dụng công thức:

Dạng 3: Chứng minh vuông góc. 

Phương pháp giải:

Dùng tích chất của tích vô hướng để chứng minh vuông góc:

Hoặc dùng công thức về tọa độ: 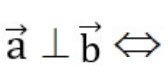  a₁b₁ + a₂b₂ = 0

Dạng 4: Chứng minh các đẳng thức về tích vô hướng hay độ dài. 

Phương pháp giải:

Áp dụng định nghĩa và tính chất của tích vô hướng, các quy tắc phân tích, biến đổi vectơ, các công thức về độ dài vectơ để biến đổi sao cho hai vế bằng nhau hoặc từ giả thiết suy ra một biểu thức luôn đúng đã được công nhận. Để chứng minh ta có thể chứng minh tích vô hướng của

với hai vectơ khác không cùng phương bằng 0.

Dạng 5: Các bài toán liên quan đến biểu thức tọa độ. 

Phương pháp giải:

Áp dụng các công thức, tính chất của tích vô hướng liên quan đến tọa độ để giải quyết các yêu cầu của đề bài.

Dạng 6: Tìm tọa độ các điểm đặc biệt trong tam giác. 

Phương pháp giải:

Áp dụng định nghĩa, tính chất, các công thức của tích vô hướng liên quan đến tọa độ, các quy tắc trung điểm, quy tắc trọng tâm để tính tọa độ điểm đặc biệt. Ta có:

– Trung điểm I (x;y) của đoạn thẳng AB với A(x_A;y_A) và B(x_A;y_A):

x =

– Trọng tâm G (x;y) của tam giác ABC với A(x_A;y_A), B(x_A;y_A) và C(x_C;y_C):

– Trực tâm H (x;y) của tam giác ABC, ta có:

Giải hệ trên ta tìm được x, y.

– Tâm đường tròn ngoại tiếp I (x;y) của tam giác ABC. Nếu tam giác ABC vuông tại A thì I là trung điểm của BC. Nếu tam giác ABC đều thì I là trọng tâm. Nếu tam giác ABC là tam giác thường thì có theo hệ 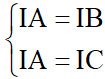hoặc gọi M, N là trung điểm của BC và AC, có hệ

Từ hệ phương trình tìm được x, y.

– Điểm D (x;y) là chân đường phân giác trong của góc A, ta có:

– Điểm E (x;y) là chân đường phân giác ngoài của góc A, ta có:

– Tâm đường tròn nội tiếp K (x;y) của tam giác ABC có BC = a, AC = b, AB = c và A(x_A;y_A), B(x_A;y_A), C(x_C;y_C). Tìm điểm D là chân đường phân giác trong của góc A của tam giác ABC. Lúc đó điểm K là chân đường phân giác trong của góc B của tam giác ABD. Hoặc dùng công thức:

(đối với bài toán trắc nghiệm).