Phép đối xứng tâm là một trong những phép biến hình hay của chương trình Hình học lớp 11. Tuy vậy, nó vẫn gây không ít khó khăn cho các bạn học sinh trong việc ứng dụng và giải toán. Bài viết này congthuctoanlyhoa.com nhằm mục đích đem lại định nghĩa, tính chất và bài tập kèm lời giải rõ ràng, dễ hiểu để giúp các bạn vượt qua nội dung học về phép đối xứng tâm này.
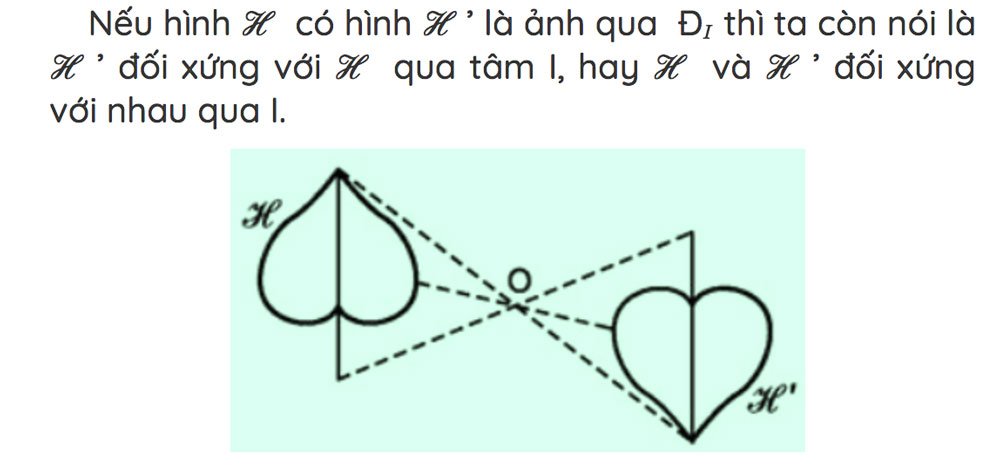
Phép đối xứng tâm là gì?
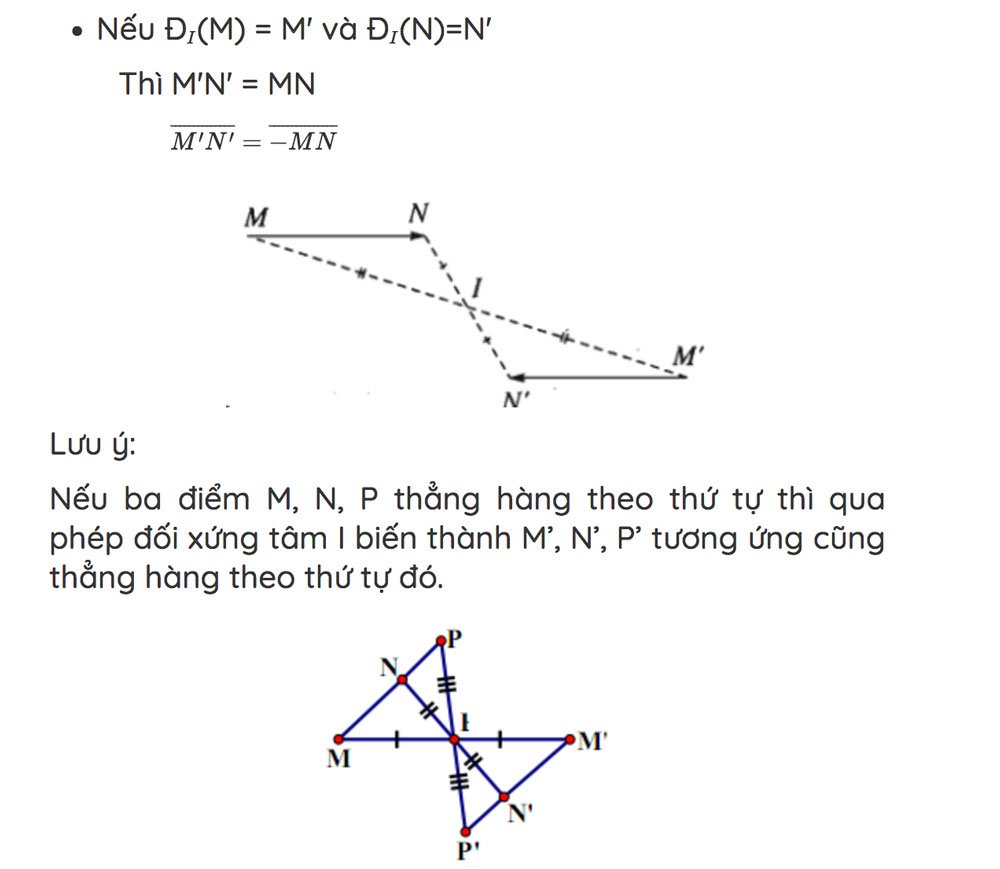
Công thức phép đối xứng tâm
Biểu diễn ảnh qua phép đối xứng tâm
Tính chất phép đối xứng tâm
Tính chất 2
- Bảo toàn khoảng cách giữa 2 điểm
- Chuyển thành một đường thẳng thành đường thẳng song song hoặc trùng với nó
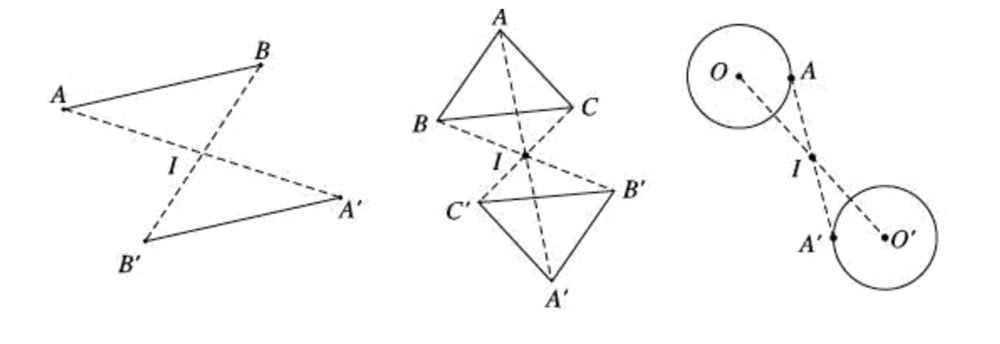
- Chuyển một đoạn thẳng thành đoạn thẳng bằng với đoạn thẳng đó
- Chuyển một tam giác thành tam giác bằng tam giác ban đầu
- Biến một đường tròn thành một đường tròn khác có cùng bán kính
Biểu thức tọa độ của phép đối xứng tâm
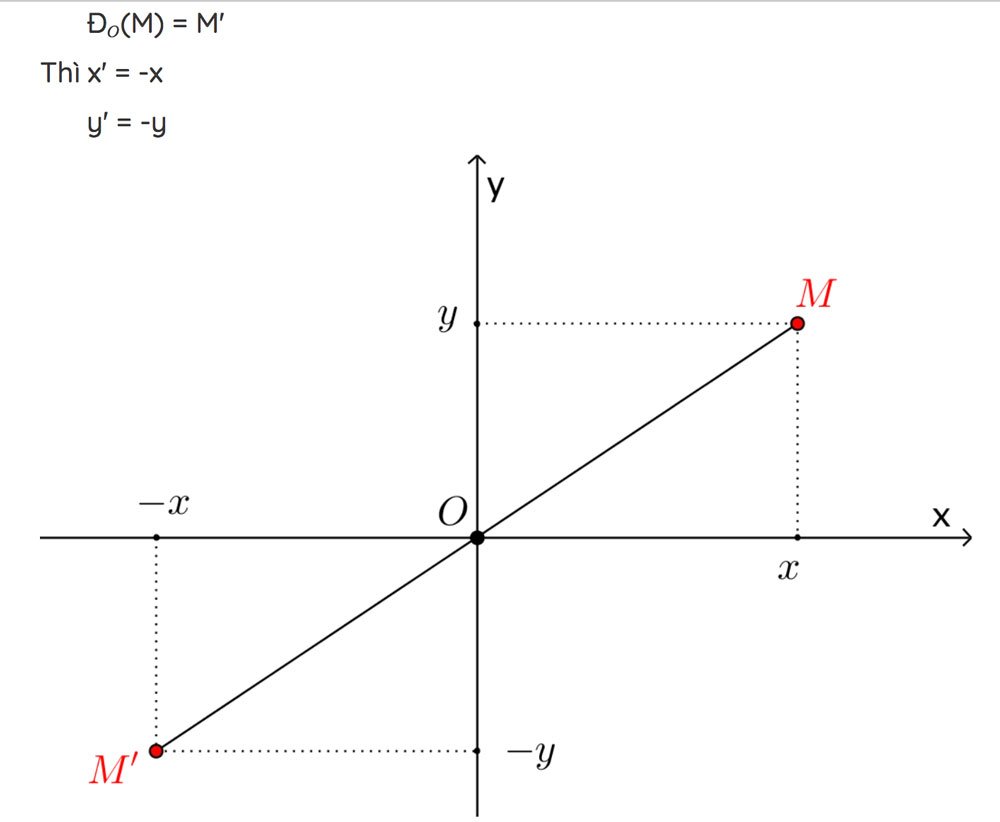
Biểu thức tọa độ của phép đối xứng qua gốc tọa độ
Trong mặt phẳng tọa độ Oxy cho M(x;y), gọi tọa điểm M'(x’;y’) là ảnh của M qua phép đối xứng tâm O, ta có:
Biểu thức tọa độ của phép đối xứng tâm bất kỳ
Gọi M'(x’;y’) là ảnh của M(x;y) trong mặt phẳng Oxy cho I(a;b), M(x;y), qua phép đối xứng tâm I thì ta có:
Tâm đối xứng của một hình
Trong Hình học 11, điểm I được gọi là tâm đối xứng của hình H nếu phép đối xứng qua I biến H thành chính nó
⇒ Ta gọi H là hình có tâm đối xứng
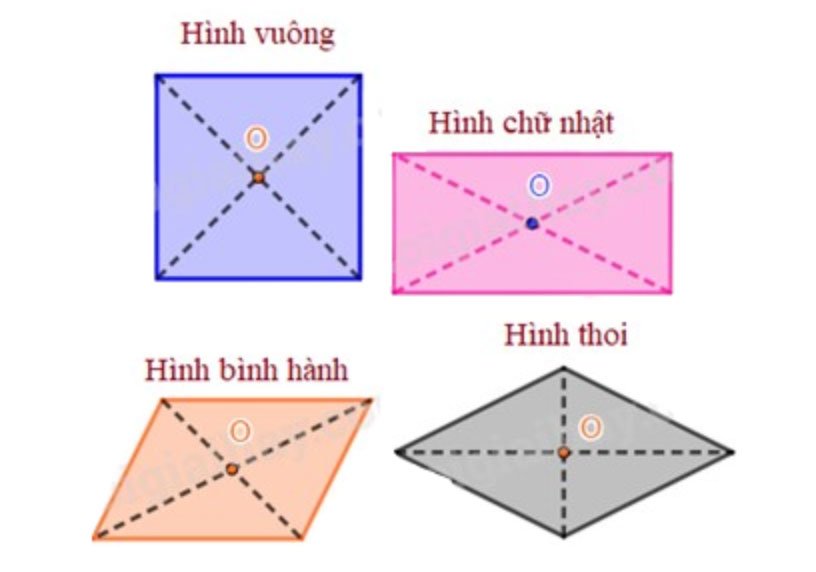
Tâm đối xứng của một số hình phẳng
Một số dạng bài tập phép đối xứng tâm kèm lời giải chi tiết
Dạng 1: Tìm ảnh của một điểm qua phép đối xứng tấm
Dạng 2: Tìm ảnh của một đường thẳng qua phép đối xứng tâm
Dạng 3: Tìm ảnh của đường tròn qua phép đối xứng tâm
Phương pháp giải
PP1: Sử dụng tính chất: Phép đối xứng tâm biến đường tròn thành đường tròn có cùng bán kính.
Bước 1. Xác định tâm I , bán kính R của (C)
Bước 2. Tìm ảnh I’ của tâm I qua phép đối xứng tâm
Bước 3. Viết phương trình đường tròn có tâm I’ và bán kính R’=R
PP2: Sử dụng biểu thức tọa độ (Phương pháp quỹ tích)
Bài tập và cách giải phép đối xứng tâm
Ví dụ 1: Trong mặt phẳng tọa độ Oxy, tìm phương trình đường tròn (C’) là ảnh của đường tròn (C): (x – 5)2 + (y + 3)2 = 16 qua phép đối xứng tâm O(0;0).
Hướng dẫn giải:
Gọi I’ là điểm đối xứng của I(5;-3) qua tâm O(0;0), suy ra I'(-5;3).
Phép đối xứng tâm bảo toàn khoảng cách nên R’ = R = 4
Vậy đường tròn (C’) có tâm I'(-5;3), bán kính R’ = 3 nên (C’): (x + 5)2 + (y – 3)2 = 16
Cách 2. Biểu thức tọa độ của phép đối xứng tâm O(0;0) là
Thay vào (C) ta được (-x’ – 5)2 + (-y’ + 3)2 = 16 ⇔ (x’ + 5)2 + (y’ – 3)2 = 16.
Ví dụ 2: Trong mặt phẳng Oxy cho đường tròn (O;R): x2 + y2 + 2x – 6y + 6 = 0 điểm I(1;2). Tìm ảnh của (O;R) qua phép đối xứng tâm I
Hướng dẫn giải:
Gọi M(x;y) là điểm bất kỳ thuộc (O;R) và (E). Từ công thức chuyển trục ta có:
(2 – x’)2 + (4 – y’)2 + 2(2 – x’) – 6(4 – y’) + 6 = 0
⇔ x’2 + y’2 – 6x’ – 2y’ + 6 = 0
⇔ x2 + y2 – 6x – 2y + 6 = 0
Cách 2. x2 + y2 + 2x – 6y + 6 = 0 có tâm J(-1;3), R = 2
Ta chỉ tìm J’(x;y) là ảnh của J qua phép đối xứng tâm I(1;2) bằng công thức chuyển trục tọa độ:
Do đó (O’): (x – 3)2 + (y – 1)2 = 4 là ảnh của (O;R) qua phép đối xứng tâm I.
Tổng kết
Trên đây là bài học về Phép đối xứng tâm mà congthuctoanlyhoa.com muốn gửi đến các bạn học sinh. Mong rằng nó đã giúp các bạn hiểu hơn cũng như nắm vững được lý thuyết, cách giải dạng bài tập này.