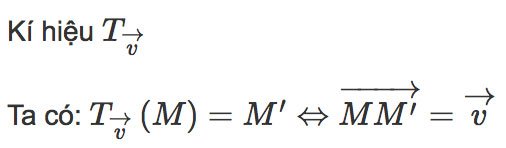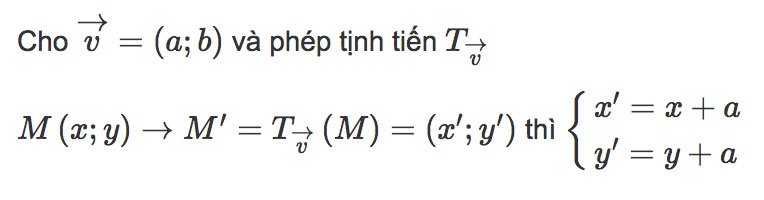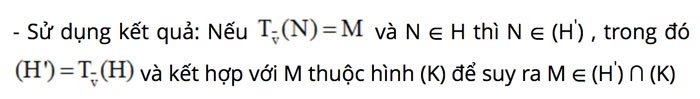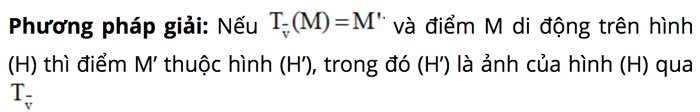[Toán 11] Phép tịnh tiến và dạng bài tập phép tịnh tiến kèm lời giải

Phép tịnh tiến là một trong những phép tính được ứng dụng nhiều trong bài tập hình học. Thế nhưng, vẫn còn nhiều học sinh nhầm lẫn và hiểu sai về phép dời hình này. Bài viết sau đây sẽ gửi đến các bạn kiến thức cũng như những dạng bài tập liên quan. Các bạn hãy cùng theo dõi nhé!

Phép tịnh tiến là gì?

Trong mặt phẳng cho vecto v. Phép biến hình biến mỗi điểm M thành M’ sao cho vecto MM’ bằng vectơ

⇒ Được gọi là phép tịnh tiến theo vector v.

Các tính chất phép tịnh tiến

Tính chất 1

Định lý 1: Nếu phép tịnh tiến biến 2 điểm M, N thành 2 điểm M’, N’ thì MN=M’N’

Nói cách khác, phép này bảo toàn khoảng cách giữa 2 điểm bất kỳ. Từ tính chất 1, ta chứng minh được tính chất sau

Tính chất 2

Định lý 2: Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính

Biểu thức tọa độ của phép tịnh tiến

Biểu thức tọa độ của phép này được xác định như sau:

Xem thêm: [Toán 11] Tổng hợp phép đối xứng tâm: Lý thuyết, bài tập chuẩn Bộ GD

Các dạng bài tập phép tịnh tiến

Sau đây là một số dạng bài kèm ví dụ chi tiết trong chương trình Hình học 11 để các bạn nắm được rõ hơn.

Dạng 1: Tìm ảnh, tạo ảnh của đường thẳng d qua một phép tịnh tiến theo vectơ v

Tìm ảnh của đường thẳng d qua một phép tịnh tiến theo vectơ v

• Phương pháp:
  • Lấy M trên d
  • Tìm ảnh M’ của M
  • d’ là đường thẳng qua M’ và song song hoặc trùng d.

Tìm tạo ảnh của đường thẳng d qua một phép tịnh tiến theo vectơ v.

• Phương pháp:
  • Lấy M’ trên d’.
  • Tìm M sao cho M’ là ảnh của M.
  • d là đường thẳng qua M và song song hoặc trùng d.

Dạng 2: Tìm ảnh, tạo ảnh của đường tròn qua phép tịnh tiến

Tìm ảnh của đường tròn (C) qua một phép tịnh tiến theo vectơ v.

• Phương pháp
  • Tìm tâm I và bán kính R’ của đường tròn (C).
  • Tìm ảnh I’ của I qua phép tịnh tiến này.
  • Đường tròn (C’) là ảnh của (C) là đường tròn có tâm I’ và bán kính .

Ví dụ: Cho đường tròn (C) có tâm I (-2; 3)  và bán kính . Viết phương trình đường tròn (C) là ảnh của (C) qua phép tịnh tiến theo vectơ u (2; -3).

Lời giải

(C) có tâm I (-2; 3)  và bán kính R = 5

Dạng 3: Tìm ảnh, tạo ảnh của một đường cong (khác các dạng trên) qua một phép tịnh tiến

Tìm ảnh của một đường cong (P) qua một phép tịnh tiến theo u (a; b)

Phương pháp

Tìm tạo ảnh của một đường cong (P) qua một phép tịnh tiến theo vectơ u (a; b)

Dạng 4: Xác định phép tịnh tiến

Vậy có duy nhất một phép tịnh tiến biến parabol (Q) thành parabol (P), theo vectơ u (1;1).

Xem thêm: [Toán 11] Công thức phép vị tự và bài tập có lời giải CHUẨN

Bài tập kèm cách giải phép tịnh tiến

Sau đây là một số dạng bài tập kèm lời giải chi tiết để các bạn học sinh tham khảo

Tổng kết

Trên đây là hệ thống kiến thức căn bản cho bài mở đầu của Hình học 11, Phép tịnh tiến. Hy vọng bài viết của Công Thức Toán Lý Hóa này sẽ giúp các bạn học sinh hiểu được thêm về phép biến hình dời hình cũng như các lý thuyết và bài tập liên quan đến bài học này. Chúc các bạn có những giờ học bổ ích với phân môn này cũng như đạt điểm cao trong các kỳ thi sắp tới.