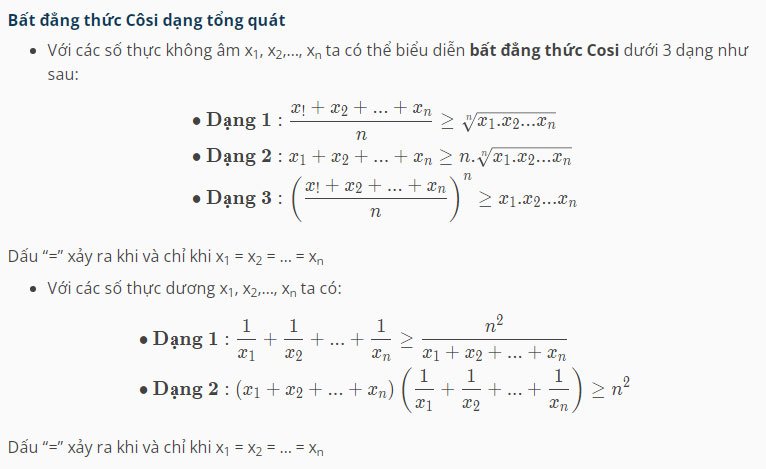[Toán 10] Bất đẳng thức Cosi – chuẩn công thức và bài giải chi tiết

Bất đẳng thức Cosi thuộc kiến thức Toán 10 được nhận định là khá quan trọng. Tuy nhiên trong quá trình học thì lại khá khó nhớ và khó hiểu. Bài viết dưới đây, congthuctoanlyhoa.com sẽ giới thiệu cho các bạn toàn bộ tổng hợp về công thức, cách thể hiện, hệ quả, cách chứng minh và các dạng toán của bất đẳng thức Cosi.

Mục lục

Lý thuyết về bất đẳng thức Cosi

Định nghĩa bất đẳng thức Cosi

Bất đẳng thức Cosi có tên chính xác là bất đẳng thức AM-GM (viết tắt của Arithmetic Mean và Geometric Mean), là bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm. Trong đó, trung bình cộng của n số thực không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng. Trung bình cộng chỉ bằng trung bình nhân khi và chỉ khi n số đó bằng nhau.

Bất đẳng thức này cũng được biết đến với tên bất đẳng thức Cauchy. Không phải do Cauchy phát hiện ra nhưng có lẽ do cách chứng minh của ông là độc đáo nhất nên bất đẳng thức này cũng được gọi bằng tên của ông.

Bất đẳng thức Cosi được biểu diễn như thế nào

Bất đẳng thức Cosi được biểu diễn dưới nhiều dạng khác nhau, tui nhiên có thể chia thành 2 nhóm chính là: biểu diễn dạng tổng quát và biểu diễn dạng đặc biệt.

Bất đẳng thức dạng tổng quát

Cho $displaystyle {{x}_{1}},{{x}_{2}},{{x}_{3}}ldots {{x}_{n}}$ là các số thực dương ta có:

Bất đẳng thức dạng đặc biệt

Đây là các trường hợp đặc biệt, cụ thể hơn dạng tổng quát ở trên khi có n cụ thể như n=2, n=3

Hệ quả của bất đẳng thức Cosi

Từ công thức dạng tổng quát và các dạng đặc biệt, ta có 2 hệ quả quan trọng của bất đẳng thức Cosi dưới đây. Các hệ quả này thường được áp dụng nhiều trong việc tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức.

Hệ quả 1: Nếu tổng của 2 số dương không đổi thì tích của chúng lớn nhất khi 2 số đó bằng nhau.
Hệ quả 2: Nếu tích của 2 số dương không đổi thì tổng của 2 số này nhỏ nhất khi 2 số đó bằng nhau.

Một số bất đẳng thức được suy ra từ BĐT Cosi như sau:

+ Tổng của một số dương với nghịch đảo của nó lớn hơn hoặc bằng 2.

$a + \frac{1}{a} \geq 2$ , $\forall a > 0$

+ Nếu x, y cùng dương và có tổng không đổi thì tích (xy) lớn nhất khi và chỉ khi x = y.

+ Trong tất cả các hình chữ nhật có cùng chu vi, hình vuông có diện tích lớn nhất.

+ Nếu x, y cùng dương và có tích không đổi thì tổng (x + y) nhỏ nhất khi và chỉ khi x = y.

+ Trong tất cả các hình chữ nhật có cùng diện tích, hình vuông có chu vi nhỏ nhất.

Các lưu ý khi sử dụng

Khi sử dụng bất đẳng thức Cosi trong chương trình Đại số 10 thì có những lưu ý như sau:

Khi áp dụng BĐT Cosi thì các số phải thỏa mãn điều kiện là số không âm
Áp dụng BĐT Cosi khi trong bất đẳng thức có tổng tích cần chứng minh
Dấu bằng xảy ra khi và chỉ khi các số bằng nhau

Ứng dụng của BĐT Cô-si

Bất đẳng thức Cosi, còn được gọi là bất đẳng thức Cauchy, là một công cụ toán học mạnh mẽ được sử dụng rộng rãi để giải quyết nhiều bài toán khác nhau, đặc biệt trong việc tìm giá trị nhỏ nhất và lớn nhất của các hàm số. Dưới đây là một số ví dụ điển hình về ứng dụng của bất đẳng thức này.

– Giải phương trình và hệ phương trình: Bất đẳng thức Cosi có thể được áp dụng để đơn giản hóa và giải các phương trình hoặc hệ phương trình bằng cách thiết lập mối liên hệ giữa các biến số, từ đó đưa ra các điều kiện cho nghiệm.

– Chứng minh các bất đẳng thức: Trong nhiều trường hợp, bất đẳng thức Cosi được sử dụng để chứng minh một số bất đẳng thức khác. Ví dụ, ta có thể sử dụng nó để chứng minh rằng tổng bình phương của các biến lớn hơn hoặc bằng tích của chúng.

– Tìm giá trị lớn nhất và nhỏ nhất của các biểu thức: Bất đẳng thức này cũng rất hữu ích trong việc tìm giá trị lớn nhất và nhỏ nhất của các biểu thức, đặc biệt trong các bài toán liên quan đến các hàm số và các biến số.

Tóm lại, bất đẳng thức Cosi không chỉ là một công cụ lý thuyết mà còn là một phương pháp thiết thực trong việc giải quyết và chứng minh nhiều vấn đề toán học phức tạp. Sự hiểu biết và áp dụng thành thạo bất đẳng thức này có thể mở rộng khả năng giải toán và phân tích toán học của người học.

Các dạng bài tập của bất đẳng thức Cosi

Để áp dụng BĐT Cosi, ta thường dùng các kĩ thuật sau đây:

Kĩ thuật chọn điểm rơi trong đánh giá từ trung bình cộng sang trung bình nhân
Kĩ thuật ghép cặp, thêm bớt
Kỹ thuật Cosi ngược dấu

Dạng 1: Áp dụng bất đẳng thức Cosi trực tiếp

Dưới đây là một số ví dụ về áp dụng trực tiếp BĐT Cosi vào bài toán

Phương pháp giải:

Để chứng minh $A \geq B$ (hoặc A > B), ta làm các bước sau:

Bước 1: xét hiệu A – B.

Bước 2: chứng minh $A - B \geq 0$ ( hoặc A – B > 0).

Sử dụng linh hoạt kiến thức ở phần lý thuyết để chứng minh ở bước 2.

Bước 3: kết luận.

Bước 4: xét A = B khi nào?

Dạng 2: Áp dụng bất đẳng thức Cosi có biến đối nhân chia thêm bớt

Phương pháp giải:

Một số chú ý khi sử dụng bất đẳng thức Cô-si:

– Khi áp dụng bất đẳng thức Cô-si thì các số phải là những số không âm

– Bất đẳng thức Cô-si thường được áp dụng khi trong bất đẳng thức cần chứng minh có tổng và tích

– Điều kiện xảy ra dấu “=” là các số bằng nhau

– Bất đẳng thức Cô-si còn có hình thức khác thường hay sử dụng:

Đối với hai số: $x^{2} + y^{2} \geq 2 x y; x + y \geq 2 \sqrt{x y}$ $x; y \geq 0$

Đối với ba số:

$a b c \leq \frac{a^{3} + b^{3} + c^{3}}{3}$ với mọi $a; b; c \geq 0$

Tổng kết

Trên đây là những kiến thức quan trọng về công thức, hệ quả, cách chứng minh cũng như các dạng toán của bất đẳng thức Cosi. congthuctoanlyhoa.com hi vọng thông qua bài viết này, bạn đọc đã có thể nắm vững kiến thức và tự tin giải các bài tập.