Bất phương trình bậc hai là một trong những chủ đề trọng tâm của chương trình Toán lớp 10, nằm trong chương 3 – Phương trình và hệ phương trình theo SGK của Bộ Giáo dục và Đào tạo (Bộ GD&ĐT). Đây không chỉ là nền tảng cho các chương sau về hàm số bậc hai, mà còn là phần kiến thức xuất hiện đều đặn trong đề thi THPT Quốc gia, chiếm từ 5–10% tổng điểm phần Đại số.
Việc nắm chắc phương pháp giải bất phương trình bậc hai lớp 10 giúp bạn không chỉ làm chủ bài kiểm tra học kỳ mà còn áp dụng vào các bài toán thực tế, đặc biệt là các bài toán tối ưu hóa giá trị biểu thức.
Bài viết này congthuctoanlyhoa tổng hợp đầy đủ lý thuyết, phương pháp giải, cùng bài tập từ cơ bản đến nâng cao có lời giải chi tiết. Toàn bộ nội dung dựa trên SGK Toán 10 (trang 65–70) và đề thi THPT Quốc gia các năm gần đây (2023–2025).
1. Lý Thuyết Cơ Bản Về Bất Phương Trình Bậc Hai
1.1. Định nghĩa
Bất phương trình bậc hai một ẩn là bất phương trình có dạng:
- ax² + bx + c > 0
- ax² + bx + c ≥ 0
- ax² + bx + c < 0
- ax² + bx + c ≤ 0
Ví dụ:
- 2x² – 4x + 1 > 0
- x² + 3x – 4 ≤ 0
Mục tiêu là tìm tập nghiệm – các giá trị của x thỏa mãn bất phương trình.
1.2. Tính chất cơ bản
-
Dấu của a quyết định chiều cong của parabol (hàm số y = ax² + bx + c)
-
Nếu a > 0, parabol hướng lên.
-
Nếu a < 0, parabol hướng xuống.
-
-
Biệt thức Δ (delta): Δ = b² – 4ac ảnh hưởng đến nghiệm của phương trình ax² + bx + c = 0, từ đó tác động đến bất phương trình.
-
Nghiệm: Dựa vào nghiệm của phương trình tương ứng để xét dấu.
1.3. Các trường hợp của Δ
| Trường hợp | Số nghiệm | Dạng parabol | Kết luận dấu của ax² + bx + c |
|---|---|---|---|
| Δ > 0 | 2 nghiệm phân biệt x₁, x₂ | Cắt trục hoành tại 2 điểm | Biểu thức đổi dấu tại x₁, x₂ |
| Δ = 0 | Nghiệm kép x₀ | Tiếp xúc trục hoành | Giữ dấu, chỉ bằng 0 tại x₀ |
| Δ < 0 | Vô nghiệm | Không cắt trục hoành | Dấu không đổi trên R |
2. Phương Pháp Giải Bất Phương Trình Bậc Hai
Có hai phương pháp chính:
-
Dùng bảng xét dấu biểu thức.
-
Dùng đồ thị parabol.
2.1. Phương pháp 1: Xét dấu biểu thức
Các bước thực hiện:
1/ Giải phương trình bậc hai: ax² + bx + c = 0:
- Tính Δ = b² – 4ac.
- Nếu Δ ≥ 0, tìm nghiệm x₁, x₂ (hoặc nghiệm kép x₀).
2/ Lập bảng xét dấu:
- Chia trục số thành các khoảng bởi nghiệm (x₁, x₂).
- Xét dấu ax² + bx + c trong mỗi khoảng, dựa trên hệ số a.
3/ Kết luận tập nghiệm:
- Lấy các khoảng thỏa mãn dấu (> 0, < 0, v.v.).
- Nếu có dấu bằng (≥, ≤), kiểm tra cả nghiệm x₁, x₂.
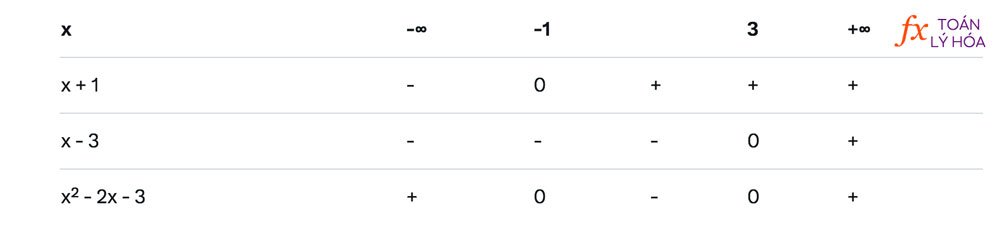
Ví dụ: Giải bất phương trình x² – 2x – 3 > 0.
- Bước 1: Giải x² – 2x – 3 = 0 → Δ = (-2)² – 4·1·(-3) = 16 → x₁ = -1, x₂ = 3.
- Bước 2: Bảng xét dấu (a = 1 > 0):
- Bước 3: Bất phương trình > 0 → Nghiệm: x < -1 hoặc x > 3.
Tập nghiệm: (-∞; -1) ∪ (3; +∞).
2.2. Phương pháp 2: Dùng đồ thị hàm số
Dựa vào hình dạng parabol y = ax² + bx + c:
-
Nếu a > 0 → parabol hướng lên → phần trên trục hoành ứng với >0> 0.
-
Nếu a < 0 → parabol hướng xuống → phần dưới trục hoành ứng với <0< 0.
Cách làm:
-
Vẽ đồ thị y = ax² + bx + c (xác định đỉnh và giao điểm trục hoành).
-
Dựa vào vị trí parabol để tìm khoảng thỏa mãn điều kiện (>0, <0).
2.3. Trường hợp đặc biệt
-
Δ < 0:
Không có nghiệm thực. Dấu biểu thức không đổi:-
Nếu a > 0 → luôn > 0.
-
Nếu a < 0 → luôn < 0.
-
-
Δ = 0:
Nghiệm kép x₀ → chỉ đổi dấu bằng tại x₀. -
Hệ bất phương trình:
Lấy giao nghiệm của các bất phương trình thành phần.
3. Bài Tập Bất Phương Trình Bậc Hai Lớp 10 Có Lời Giải
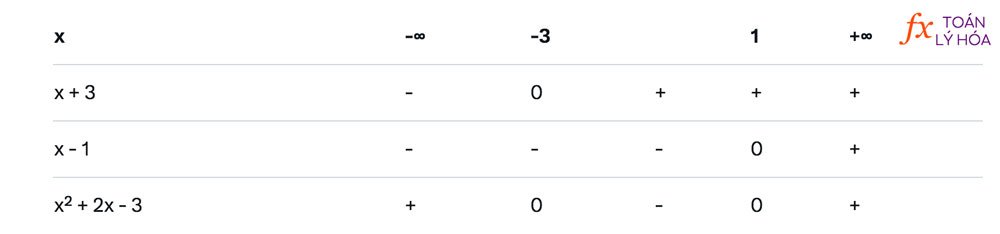
Bài 1 (SGK):
Giải:
- Phương trình: 2x² + 4x – 6 = 0 → x² + 2x – 3 = 0.
- Δ = 2² – 4·1·(-3) = 16 → x₁ = -3, x₂ = 1.
- Bảng xét dấu (a = 1 > 0):
- Bất phương trình ≤ 0 → Nghiệm: -3 ≤ x ≤ 1.
Đáp án: [-3; 1].
Bài 2:
Giải:
- Phương trình: x² – 6x + 9 = (x – 3)² = 0 → Nghiệm kép x = 3, Δ = 0.
- Vì (x – 3)² ≥ 0 ∀x, và chỉ = 0 tại x = 3.
- Bất phương trình ≥ 0 → Nghiệm: ∀x ∈ ℝ.
Đáp án: ℝ.
Bài 3 (Nâng cao):(Thi THPT)
{x² – 4x + 3 > 0
2x² + x – 1 ≤ 0}
Giải:
- Bất phương trình 1: x² – 4x + 3 > 0.
- Phương trình: x² – 4x + 3 = 0 → x₁ = 1, x₂ = 3 (Δ = 16).
- Bảng xét dấu (a = 1 > 0): Nghiệm x < 1 hoặc x > 3.
- Tập nghiệm: (-∞; 1) ∪ (3; +∞).
- Bất phương trình 2: 2x² + x – 1 ≤ 0.
- Phương trình: 2x² + x – 1 = 0 → x₁ = -1, x₂ = 1/2 (Δ = 9).
- Bảng xét dấu (a = 2 > 0): Nghiệm -1 ≤ x ≤ 1/2.
- Tập nghiệm: [-1; 1/2].
- Giao nghiệm: (-∞; 1) ∪ (3; +∞) ∩ [-1; 1/2] = [-1; 1/2].
Đáp án: [-1; 1/2].
Bài 4:
Giải:
- Yêu cầu: x² – 2mx + m – 1 > 0 ∀x → Δ < 0 và a > 0.
- Đây là hàm bậc hai với a = 1 > 0.
- Tính Δ = (-2m)² – 4·1·(m – 1) = 4m² – 4m + 4 = 4(m² – m + 1).
- Δ < 0 → m² – m + 1 < 0.
- Xét phương trình m² – m + 1 = 0 → Δ’ = 1 – 4 = -3 < 0 → m² – m + 1 > 0 ∀m.
- Vậy không có m thỏa mãn Δ < 0 → Bất phương trình không có nghiệm ∀x.
Đáp án: Không có m.
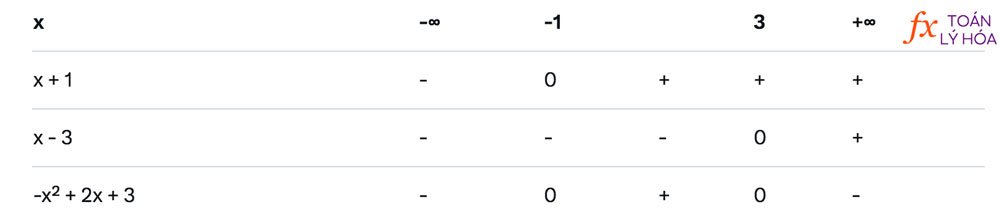
Bài 5:
Giải:
- Phương trình: -x² + 2x + 3 = 0 → x² – 2x – 3 = 0 → x₁ = -1, x₂ = 3.
- Bảng xét dấu (a = -1 < 0):
- Bất phương trình < 0 → Nghiệm: x < -1 hoặc x > 3.
Đáp án: (-∞; -1) ∪ (3; +∞).
4. Mẹo Giải Nhanh Và Ôn Thi Hiệu Quả
✅ Luôn tính Δ trước để xác định số nghiệm.
✅ Nhớ chiều parabol theo dấu của a.
✅ Khi giải hệ, nên vẽ trục số và lấy giao nghiệm trực quan.
✅ Dùng máy tính Casio fx-570VN Plus để kiểm tra nghiệm nhanh.
5. Kết Luận
Bất phương trình bậc hai lớp 10 là phần kiến thức nền tảng, giúp bạn hiểu sâu hơn về hàm số bậc hai, đồ thị parabol và chuẩn bị tốt cho các bài toán khó hơn ở lớp 11–12.
Hãy luyện tập nhiều dạng bài, đặc biệt là các bài có tham số m và bất phương trình chứa nghiệm kép, để làm chủ phần này trong các kỳ thi.
Nếu bạn thấy bài viết hữu ích, hãy chia sẻ cho bạn bè nhé.
FAQ – Câu Hỏi Thường Gặp
1. Bất phương trình bậc hai là gì?
Là bất phương trình có dạng ax² + bx + c > 0 (hoặc <, ≥, ≤), với a ≠ 0.
2. Làm sao biết bất phương trình có nghiệm?
Tính Δ = b² – 4ac và xét dấu biểu thức theo hệ số a.
3. Cách vẽ đồ thị nhanh?
Xác định a (hướng parabol), tìm đỉnh (-b/2a), giao điểm trục hoành (x₁, x₂).
4. Bất phương trình bậc hai có trong đề thi THPT không?
Có – thường xuất hiện 1–2 câu, đặc biệt dạng kết hợp với hàm số hoặc hệ bất phương trình.
5. Mẹo tránh sai khi xét dấu?
Đừng quên đổi dấu khi nhân hai vế với số âm và luôn kiểm tra nghiệm vào bất phương trình trước khi kết luận.